90% получа-

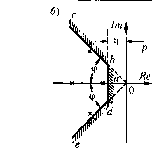Рис. 8.8

Соответственно при С, ем р 2,72.

Зала1Н1еонреле.тениой колебательности заставляет ограничивать область расположения корней двумя лучами (рис, 8.8, а), которые составляют с осью вещественных угол

ф = arctg (Р/а) = arctg р.. (8.43)

Колебательность системы можно определить без нахождения корней характеристического уравнения подобно тому, как это было сделано выше но отношению-к степени устойчивости. Идея метода заключается в том, что используется иодстановкар =J2e которая соответствует повороту координатных осей (рис. 8.8, б) против часовой стрелки на угол п/2 - ф. При это.м ио крайней мере один корень попадает на .мнимую ось и зате.м он отыскивается. Ввиду громоздкости этот метод почти пе и.меет практического значения.

При задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной пря.мой, проходяи1ей параллельно мни.мой оси ш расстоянии г\ (рис. 8.8, б). Расположению корней в этой области соответствует выдерживание требуемого запаса устойчивости, определяемого величиной колебательности р, или затуханием,-и требуемой степени устойчивости У], характеризующей быстродействие системы.

Для определения параметров систе.мы, при которых обеспечивается нахождение корней характеристического уравнения в заданной области, можно воспользоваться £>-разбнением. В это.м случае в плоскости двух параметров системы может быть построена область, аналогично построению области устойчивости (см. гл. 6).

Использование корней характеристического уравнения для оценки качества yir-равления является пе совсем полным, так как вид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения. Для того чтобы учесть это обстоятельство, рассмотри.м, например, зависимость между управляемой величи!юй и задающим воздействием, записанную посредством передаточной функции за,мкнутой системы (5.20):

У(р) = Ф(р)С(р) =

W(p) \ + W(p)

G{p).

Передаточная функция замкнутой системы представляет собой дробнорацио-на.чьпую функцию

Z)(p) аоР +а,р -+... + Раскладывая числитель и знаменатель (8.44) па .множители, получим

ф(р)-(р-р5Хр-Р2)-(р-р )

a{V-Ps){V-Pi)-{p-Pn)

(8.44)

о,) р

= Р}1--=-рг- (8.48)

Здесь использовано поиятие с]зедпегеометрического корня (8.26):

Корпи числителя pf,.р называются нулями передаточной функ1Н1и, так как

в точке р р? передаточная фугнсция обран1ается в нуль. Корни знаменателя р

р являются корнями характеристического уравнения, и опн называются полюсами передаточной функции. В полюсе, т. е. при р =р передаточная функция обращается в бескопечиость.

Полюсы передаточной функции ха[зактеризуют левую часть дифференциального уравнения, а пули - правую. В частном случае, когда передаточная функщчя (8.44) не имеет плей, правая часть ди4)ференциа..ты10го уравнения имеет вид В(р) f{t) = = bJ{L) и формула (8.45) сводится к выражению

В этом случае вид переходного П[зоцесса определяется только расположепие.м полюсов.

Зада1П1е области расположения полюсов и нулей позволяет более полно оцешггь вид переходного процесса. Пе останавливаясь па подробном анализе, П[зиведем без доказательства обппю рекомендации, которых желательно 1рпде]зживаться при выборе расположения полюсов и пулей передаточных функций [70].

1. Желательно располагать ну.чи вблизи об.тасти расположения полюсов. Удаление нулей от области полюсов ведет к увеличепню а.мплитуд собствепных колебаний в переходном процессе.

2. Для умещзшения отклонений в переходно.м процессе часто бывает выгодно удалять полюсы друг от друга,

3. Приближоте друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мни.мой оси.

Кроме этих рекоменда1П1Й сохра}1ЯЮт свою силу ограничения па область расположения полюсов, накладываемые в связи с требовапия.ми обеспечения опреде;ен-ного запаса устойчивости и быстродействия (см. рис. 8.8, б).

§ 8.6. Диаграмма Вышнеградского

Рассмотри.м характеристическое уравноню третьего порядка

flflp + aj) + ар + % = 0. (8.47)

Приведем eio к нормированному 1!иду. Для этого разделим все члены на а, и введем новую переменную

В результате получим нормированное уравнение г/ + л/ + + 1 = О, (8.49)

где коэффициенты

А) 2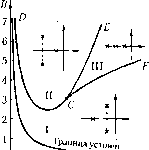

1В0СТИ

12 3 4

Рис. 8.9

6 7

называются параметрами Вгяшнеградского.

На плоскости параметров An В нанесем границу устойчивости. Условия устойчивости системы третьего норядкабьии впервыссформули1Х)ваны Вышпеград-ским cuie в 1876 году, до появления в 1895 году критерия Гурвица. Эти условия: Л > О, Л > О и ЛВ > 1. Уравнение границы устойчивости (колебательной): АВ = 1 при Л > О и В > 0. Это есть равиобокая гипе[)-бола, для которой оси координат служат асимнтота\н1 (рис. 8.9). Область устойчивости системы, согласно написанны.м вьине условня.м, лежит выше это!! кривой.

Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического урашюиия. Замети.м, что в тючке С, где Л = 3 и В = 3, характеристическое уравнение (8.49) принимает вид (q + 1) = 0. Следовательно, в этой точке все три корня равны: q, = q2 Яз ° При .этом для исходного характеристического уравнения согласно (8.48) получаем р, Р2 =

В общем случае возможны два варианта: 1) все три корня веществетыс; 2) один корень вещественный и два ко.мплексных.

Граница между этими двумя случая.ми определяется равепство.м нулю дискриминанта уравнения третьей степени (8.49), который может быть получен, напри.мер, из фор.мулы Кардана для решения кубического уравнения

А~В -4{А + В) + 18ЛВ - 27=0.

.Это уравнение дает на плоскости параметров Л, В две кривые: СЕн СЕ(рис. 8.9). Внутри области /.- С/ дискриминант гюложитслсн. Следовательно, в этой области и.vIeeтcя три вещественных корня (область HI). В остальной части плоскости диск-ри.мииапт отрицателен, что соответствует наличию пары ко.мплексных корней.

Существенное значение и.меет взаимное расположение веществстюго и комплексных корней. Будем различать здесь два случая: I - пара комплексных корней лежит ближе к .мнимой оси, чем вещественный, и II - вен1ествеппый корень лежит ближе к .мнимой оси, чем пара ко.мплексных. Границей между этими дву.мя случаями является расположение всех трех корней на одинаково.м расстоянии от мнимой оси. Уравнеиие этой границы .можно пайти, положив зиачепня корней с/, = -а, и с/г.з = = -а ±7Р, Тогда характеристическое уравпепис (8,49) будет

q + Aq + Bq+ i

(q + a)(q+a-j)iq+a+j?,) I- a (a + p) = 0.

q +?.aq+{3a?+ P) q +