F(x) ky signx.

(18.83)

Поскольку движение предполагается без остановок, то нелинейную функцию (18.83) подвергаем гармонической линеаризации, как релейную характеристику, и на ос11овании фор.мулы (18.18), полагая х = а sin ю/, иолучае.м

(18.84)

где а - амплитуда колебаний скорости х = рР; амплитуда колебаний самого угла Р при зто.м, очевидно, будет

Р = -cosco ю

Выражение (18.84) представляет собой известную формулу линеаризации сухого трения с иомоии>ю вибраций, Найде.м условия, ггри которых она здесь стграведлива. Согласно (18.81) и (18.82) имеем

откуда

что и является условием, при котором справедливо дальнейшее решение.

Характеристическое уравпение всей замкнутой системы согласно (18.82), (18.84) и (16.53) получает вид

{Т,р + p + k т,р + 1)бР + k,k + (Г р + \){Т,р + \)р = 0. ла

После подстановкир =/ю получаем

0)2=0,

fAky па

+ k\ +1

ш-7;г,у =0.

Чтобы исследовать влияние коэффициента к на динамику системы, выразим из этих двух уравнении величины к и а через ю:

Ак-,

я(Г ГХ-1-,б)

(18.87)

За.\гетнм, что а = °° ири

(со ),. ----, Ф-

\ о в./

Изменяя й), в интервале (ю ), < ю < + строим ио формулам (18.87) график а = !{к), представленный на рис, 18.16, б. Условие, ири котором справедливо это peinc-нис, было выражено неравсрютвом (18.85), Подставив в пего значения а = а и ю = ю из (18,87), приводим его к виду

b-2U\ + k,k,)

п>1,

(18,89)

b = 4l]+Ak,kTX-T .

Для исследования устойчивости найденного периодического решения на основании (18,86) находим

ЭX да

>0,

<0,

<0,

<0,

Критерий (18.6.3) при этом не вьпю.пшстся, что означает неустойчивость найденного периодического ре1пения. Это и показано условно вертикальными стрелками на рис, 18,16,6.

Легко проверить, что значение (18,88) совпадает с границей устойчивости ли- нейной системы без сухого трения. Следовательно, добавление сухого трения несколько распшряет область устойчивости системы, но весьма своеобразно, а и.\гсппо: неустойчивость найденного периодического решения означает, что при к > й р и при выполпении условия (18,89) система может быть устойчивой в малом (при начальных ус,;ювиях, которые дают начачьную амплитуду собственных колебаний системы в переходпо.м процессе, лежащую ниже кривой на рис, 18.16,6), Однако система неустойчива в большом (при начальных aилитyдax собственных колебаний выше этой кривой). Последнее можно об1>яспить физически тем, что при больших амплитудах и соответственно ири больших скоростях движения демпфирующее влияние силы сухого трения, которая сохраняет одну и ту же величину при любой скорости, становится несущественным, вследствие чего система оказывается неустойчивой, как и при отсутствии сухого трения.

-со

При певыполпсиии условия (18.89) требуется исследование обоих уравнений (16.52) coB.viecTHO (это будет уже нелинейность второго класса, так как OFia затрагивает обе величины: входную и выходную Р). При ;этом колебания угла Р будут происходить с остановками. Это - задача более сложная.

Пример 3. Пусть теперь в той же систе.ме действует не сухое трение, а сопротивленне двпже1и1ю объекта, пропорцио-налыюе квадрату скорости, с линейной составляюн1ей (рис. 18.17, а). Уравнение управляе.мого объекта с двигателем имеет в этом случае вид (16.63). Перепишем .здесь его иначе но аналогии с предыдуиим при.меро.%г

(Г /; +l)x-f(x) = ,/ х = рР, (18.90)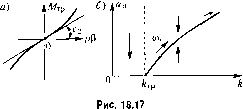

Полагая X = asin со, гю формулам гармонической линеаризации (18.10) получаем

9 = -

;fa2sin2\/(signsini/)sin\i/ d\\i =

1 fr Ч ; 1 Г / 2 Ч 1 8/

= -\ ki,(Г тг Ц1 а \\1--A-fjrt snr \/=-

па ,i па i

Следовательно,

f(x) =

Составив, как и раиьпге, характеристическое уравнение, приходим к выраже1гиям:

а)2=0.

ш-7;гу =0,

(18,91)

откуда находим;

к = (ТМ +1), а,

к, 8/?x

(18.92)