Для нахождения Дц необходимо первый столбец определителя Д заменить на (8.63):

Ап =

2 -i О

О - 3 a

= a2(aia2- o 3) + 3 f-

По формуле (8.64) находим единственный коэффициент В = Ь. В результате получаем значение интегральной квадратичной оценки:

о

23! Аз 002-аа

(8.78)

Это выражение и служит для выбора параметров системы, входящих в коэффициенты н 2> З условия минимума величины I.

Посг1)Оим диаграмму квадратичной интегральной оценки па плоскости параметров Вышнеградского Л и В. Согласно § 8.6

fl, = Л аа-, а2=В аа. Подставив это выражение в (8.78), получим:

ЛВ-1

Найдем безразмерную оценку 7о в соответствии с фор.мулой (8.57). Подставляя

значение среднегеометрического корпя

1л ---

получаем

ЛВ-1

(8.79)

При 7() = const это дает на плоскости параметров Выпгнегородского кривую

ЛЧ(ЛВ-1)(5-27о) = 0. (8.80)

Построенные по это.му уравнению кривые постоянных значеггий оценки 7 нанесены па диаграмме (рис. 8.17). Там же пугпстиром папесены кривые, взятые из диаграммы Вышнегородского (рис. 8.9), показывающие области колебательности (I) монотонного (II) и апериодического (III) процессов. Минимум интегральной оценки находим, приравнивая нулю частные производные:

= 0,4 = 0,

О, (АВ-\)-А = 0

что дает АВ-2

откуда находим А = 1, В = 2. Следовательно, минимум квадратичной интегральной оценки /о = 1,5 имеет место в точке D (рис. 8.17). Эта точка лежит, однако, слигиком бли,зко к границе устойчивости, что может не обеспечить необходимого запаса устойчивости (см., например, рис. 8.12). Практически лучше брать параметры системы не точно в точке D, а несколько правее и выше.

Этот результат имеет смысл, однако, только в тех случаях, когда Ь, а, flg остаются постоянными, а выбираемые параметры систе.мы входят только в коэффициенты а, и 2 уравнения (8.77).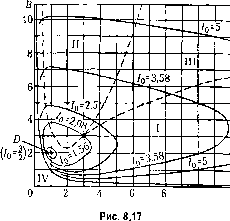

10 л

§ 8.8. Частотные критерии качества

Под частотнььми критериями качества будем понимать такие критерии, которые пе рассматривают вида переходного процесса, а базируются иа некоторых частотных свойствах системы. Частотные критерии качества особенно удобно применять при использовании частотных .методов расчета, так как при этом получается наиболее простое решение задачи.

Частотные критерии наиболее разработаны в отношении оценки запаса устойчивости замкнутой системы. Разу.меется, что при .этом система должна быть устойчивой. Запас устойчивости замкнутой системы можно определять по удалению амплитудно-фазовой характеристики разо.мкнутой системы (рис. 8.24, а) отточки (-1,;0). Для этой цели вводятся понятия запаса устойчивости по aMwiumyde (модулю) и запаса устойчивости по фазе.

Для случая, изображенного на рис. 8.18, а, удаление а. ф. х. от критической точки определяется величина.ми и, и U2, выраженными в децибсчах:

I,=201g, L2=201gf/2-

Запас устойчивости за.мкнутой систе.мы но а.мплитуде равен мини.мальпой из них:

L, = min(L L2}.

Че.м больше L, тем больше запас устойчивости по амплитуде. Система считается хо-роию демпфированной, если L, составляет примерно 6--20 дБ, что соответствует 2 10 в линейном масштабе.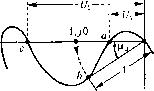

V=ImW(j03)

б) V

о UReWUoi)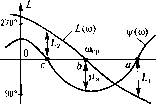

-180

Рис. 8.18

И.З рис. 8.18, а видно, что даже при С/ <Si 1, f/2 1 точка b может оказаться вб.тизи критической точки (~1,;0). Поэтому дополнительно к запасу устойчивости по амплитуде вводится запас устойчивости по фазе р.,:

p,= 180 + v

Здесь - аргу.мент (фаза) частотной передаточной ф)Ч1кции разомкнутой системы W(/(i)), соответствующий ее .\юдулю Л({1)), равному единице (точка b па рис. 8.18, а):

= ¥(ы)1л(с Ы.

Запас устойчивости замкнутой систе.мы но фазе тем больше, чем больше р,.,. В хорошо демпфированных системах он составляет около 30 + 60 .

Величины Lj и Pj могут быть определены и при использовании логарифмических частотных характеристик разомкнутой системы.

На рис. 8.18, б изображены л. ч .х., соответствующие рис. 8.18, а. Так как /.(ш) = 20 Ig W(/(i)), то в ука.занных па рис. 8.18, а точках имеем: L. < О, -180 ; L = 0, -180 < Wi, < -90 ; > О, = -180 . При ы = - модуль Z, - -оо , а фаза \\1 = -270 . Величины и L2 определяются в точках перехода л. ф. х. через ось абсцисс, а величина Рз - на частоте среза л. ф. х. щ.

Недостатко.м рассмотренного критерия является то, что для определения запаса устойчивости нсобходи.мо задать два числа: L, и pg. В этом отпопгении более удобно определять запас устойчивости по показателю колебательности. Показателем колебательности называется максимальное значение ординаты М , амплитудной характеристики замкнутой систе.мы (см. рис. 8.19) при начальной ординате, равной единице, т. е. относительная высота резонансного пика. Физически эта характеристика

представляет собой следующее. Если задающее воздействие меняется по закону g = gniax sin (Jit, то управляемая величина в режиме установившихся вынужденных колебаний будет меняться но закону у =-- у, sin (wt + \/). Отношение а.мплитуд г/ , и g a определяется модулем частотной передаточной функции замкнутой систе.\н>1:

=modO(jw) = mod-2, (8.81)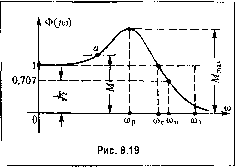