и 1

Рис. 11.2

2 4 б 8 10 12 14 16 л;

Рис. 11.3

Графически этот закон распределения изображен на рис. 11.2. Он представляет собой равновероятное распределение в некотором итггервале (в рассматриваемом случае от 1 до 6).

В некоторых случаях закон распределения случайной величины может задаваться в аналитической форме.

Примеро.м аналитического задания закона расиределения дискретной случайной величины является часто иснолызуемый закон Пуассона. Он применим к дискретным случайным величинам, которые теоретически могут принимать все положительные значения от О до оо. Примерами таких величин могут служить число пассажиров вагогга трамвая, число вызовов па телефонной станции в течение какого-либо определенного отрезка времени и т. п. Этот закон для целых значений числа .т записывается следующим образом:

Р{х) =

(11.3)

где Р {х) - вероятность появления значения х; X ггредставляет собой среднее значение данной дискретной величины, полученное по результатам больщо10 числа опытов.

Графически этот закон имеет вид, изображенный на рис. 11.3, причем место .мак-симу.ма зависит от величины X.

В качестве одного из примеров рассмотрим функцию у (С), которая .может принимать одно из значений +а или -а (рис. 11.4).

Предположим, что среднее число пере.мен знака в единицу вре.мерш этой функции равно \1 и что вероятность перемены знака па интервале (t, t + At) не зависит от того, что происходит в остальные моменты времени. Тогда вероятность перемены знака иа интервале At составит yiAt< 1. Вероятность того, что на интервале At не

произойдет перемены знака, будет (1 - \xAt).

Если взять два интервала времени At, то вероятность отсутствия перемены знака па двух интервалах будет равна произведению вероятностей и составит (1 - рАг).ДлятрехинтерваловДГонасоставит(1 - цМ) и т. д.

Возьмем теперь конечный интервал вре.мени Т, который можно представить в виде Г= nAt. Тогда веро-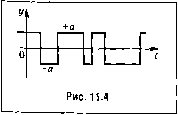

6 6 6 6 6 6j Вообще для равновероятггого закона распределения (11.5) превращается в формулу

х = - = х.

Для случайной величины, распределенной по закону Пуассона, среднее значение, подсчитанное по формуле (11.5), дает

х = Х.

Основггые свойства среднего значения случайной величины следующие. 1. Для любых сл)гчайных величин среднее значение их суммы равно сумме средних значений .этих величин:

x + y-¥z + ,.. = x-¥y + z + ...

ятность отсутствия перемены знака на этом интервале можно найти из выражеритя

P(0) = lim {\-\хМ) = 11т(1-рД0 =е.

Аналогичным образом можно показать, что вероятность одной перемены знака

на интервале Г будет Р(1) = р,Ге *, вероятность двух пере.мен знака Р(2)= е~

и т. д. Следовательно, вероятность х перемен знака па интервале времени Т будет определяться выражением

P(x)Je-\ (11.4)

которое совпадает с формулой (11.3), если положить в ней X = рГ, где рГ- среднее число перемен знака на интервале времени Г, которое будет наблюдаться при .многократном повторении наблюдения.

Хотя закон распределения полностью определяет случайную Bejni4HHy, для практики нужны некоторые более простые осредненные характеристики случайной величины, выражающиеся в виде обыкновенных неслучайных чисел.

Одной из таких характеристик является среднее значение, или математическое ожидание, случайной величины. Оно определяется из выражения

x = M[x] = JXiPi. (11,5)

Так, например, для случая бросания игральной кости

x = yx,P:=fl-- + 2--+3--+4-- + 5--+6--l--(l + 2 + 3 + 4 + 5 + 6) = -= 3,.5.

=14 f]

! = 1

есть средний квадрат случайной величиньг

Часто используется так называемое среднеквадратичное значение случайной величины, представляющее собой корень квадратный из среднего квадрата случайной величины:

Иногда рассматривается центрированное значение случайной величины Хд =х-х, где X - среднее значение. Тогда аналогично фор.муле (11,6) можно ввести понятие центрального момента т-го порядка

М[(х-х) ]= i {x.-xfP.. (11.7)

г = 1

Из формулы (11.7) следует, что центральный мо.мент первого порядка всегда равен нулю.

Обратимся теперь к характеристика,м рассеяния дискретной слу11айной величины.

Если X - случайная величина, ах - среднее значение этой величины, то величина X - X есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величинах.

2. Среднее значение произведения случайных величии, независимых друг от друга, равно произведению средних значений этих величии:

xyz...=x-y-z...

Последняя формула пе распространяется на обицш случай любых случайных величин.

В виде обобпюпия понятия среднего значения (11.5) отметим, что выражение

7 = м\х \=±хтр, (11.6)

называется моментом т-го порядка случайной величины х. В частности, момент пулевого порядка выражает свойство (11.2), и он всегда равен единипе:

Мо.мент первого порядка есть среднее значение (математическое ожидание) случайной величины (11.5). Момент второго порядка