
 |
|
|
Главная -> Повышение запаса устойчивости Дх., = Дх, + dF Эрх, Арх, -(18.55) (аналогично и для других типов пелинейпыхуравнепий), где индекс п означает, что в частные производные нужно подставить х, = а sincOnt и рх, = а со cos со /. Эти Заметим, что для систем с нелинейностью видахз = F(Xi) без гистерезисиой нетли частота СО не входит в ко;-)(()(1)иииеиты характеристического уравнения. Поэтому из уравнения (18.48) или (18,51) сра.зу определяется а.мплитудаа , а,зате.м из (18.49) или (18,52) - частота со . /1ля систем с более сложными иелинейностя.ми получаются два уравнения с двумя неизвестными. Учет временного запаздывания в нелинейной системе. В нелинейной систе.ме, как и в линейной, может иметься постоянное по времени запа,здывание т. При этом уравнение линейной части (18.31) получит вид Выражение (18.34) при этом будет Q Осо) + R (jia) (cosTCO - j .sinTCO) {q +jq )--=Q. (18.53) К уравнению (18.53) можно применить основной способ отыскания периодических решений или другой из изложенных выше. Устойчивость периодических решений. Выше уже указывалось, что не всякое ие-риодическое репнчнте уравнений собственного движения пелипейпой системы будет соответствовать автоколебаниям, а только устойчивое. В конкретных задачах часто из физических соображений бывает сразу видно, возникают автоколебания или нет. Поэтому иногда пет нужды в математическом исследовании устойчивости пайдеппого периодического решения. Однако в ряде случаев все же приходится этот вопрос исследовать. Задача исследования устойчивости периодического решения сводится, вообще говоря, к анализу линейного уравнения с периодическими переменными коэф(}1ици-ептами. А. М. .Ляпуновым 58] разработаны соответствуюнпте методы. Но их использование во .многих случаях представляет пока еще большие трудности. Поэтому здесь строгое исследование услойчивости периодических решепий излагаться не будет. Опишем три приближшшых способа исследования устойчивости периодического решения: 1) осреднение ко,э(}1фицие1ггов; 2) использование кривой .Михайлова; 3) шш-литический критерий. Осреднение коэффициентов при исследовании устойчивости периодического решения. Запишем диф(()еренциальное уравнение замкнутой системы в .MajHix оттотоне-ниях Дх от исследуемого периодического решешш: х = а sin со /,. /1ля линейной части системы наосиовании уравнения (18.31) получим Q(p)Axi = -R(j))Ax2. (18.54) Уравнение нелинейного звеиа, напримерXj = /-(Xi,px,), примет при ;том для малых отклонений вид частные производные и являются периодическими переменными коэффициентами. В задачах теории управления они .могут меняться как плавно, так и скачками (см. примеры в § 18.3). Осредпим полученные периодические коэффициенты, после чего вместо (18.55) будем иметь линейное у1)авпеиие с постоянными коэ(эфициентами Ах.,= >f(a ,(o ) + >f,(a ,(o )p]Ari, (18.,56) (7\/, 1 7п (18.57) Характеристическое уравнение систе.мы, определяющее устойчивость периодического решения, согласно (18.,54) и (18.56) будет QiP) + (Р) [ > ( . ю ) i( .(%)7J]=0. (18.58) Если оно удовлетворяет линейному критерию устойчивости, то исследуемое периодическое решепие устойчиво. В случаях, когда нелинейное звено описывается уравнением видах2 F(Xi) (с гистерезисной петлей или без нее), осреднепное характеристическое уравпспие для исследования периодического решершя будет Q(p) + /?(p)( ) = 0, (18.59) (18.60) Использование кривой МихаЬюва для исследования устойчивости периодического решения. Каждому конкретному значению а будет соответствовать определеипая кривая Михайлова (18.45). При а=а она пройдет через пачаю координат (рис. 18.9). Для исследования устойчивости периодического решения с амплитздой а = а дадим малое приращение амплитуде Да. Тогда нри а = а + Да кривая Михайлова .займет либо положение /, либо положение 2 (рис. 18.9). При этом кривая /, охватывающая начато координат, соответствует затухающи.м колебаниям переходного процесса, а кривая 2 - расходящи.мся колебаниям. Поэтому если при Да > О кривая Михайлова займет положение 1, а при Да < О - положение 2, то переходный ироцесс в системе будет таким, что колебания с амплитудой, больнгей чем а , затухают, а колебания с а.мплитудой, меньшей чем а , расходятся. Следовательно, переходный и1)оцесс с обеих сторон сходится к исследуемо.му периодическому процессу с амплитудой а . Это означает устойчивость последнего, т, е. в системе имеют 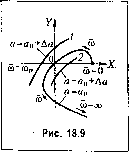 ЭХ Эа ЭК Эа (18.61) где X и Кобозиачают вещественную и мнимую части аналитического выражения кривой Михайлова, а индекс и означает подстановку а = а , м = ю .Как видно из рис. 18.10, а, для устойчивости исследуемого периодического решения вектор, оиределяе-.мый проекциями (18,61), должен лежать с определенной стороны от касателыюй МЛк кривой Михайлова, направление которой в свою очередь определяется проекциями (dY Эй (18,62) Из расположе1Нш вектора с проекциями (18,61) но отношению к вектору с проекциями (18,62) и видна непосредственно устойчивость или неустойчивость данного периодического решения с амплитудой а . На рис. 18.10, б и о показаны те же векторы, что и па рис. 18.10, а, по для других видов кривых Михайлова. Видно, что во всех случаях для устойчивости исследуемого периодического решения требуется, чтобы вектор с проекциями (18.61) лежал справа от касательной MN, если смотреть вдоль кривой Михайлова в сторону возрастания 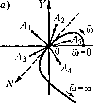 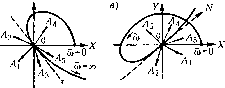 место автоколебания. Если же при Да > О получится кривая 2, а ири Да < О - кривая 1, то переходный пропесс в обе стороны расходится, т. е. исследуемое периодическое решение неустойчиво (система устойчива в малом и неустойчива в болыно.м, как па рис. 16.3, 6). Аналитический критерий устойчивости периодического решения. Развивая прс-дылупн1Й способ, видим, что пет необходимости строить сами кривые Михайлова. Все исследование можно произвести аналитически. В само.м деле, для того чтобы узнать, нри.мет ли кривая Михайлова при Да > О положе1П1е 1 (рис, 18.9), достаточ11о определить, куда будет перемепшться с увеличением а тл точка кривой Михайлова (м = ю ), которая при а = а находится в начале координат. Если она будет перемешаться по [гаправлениям O/lj, 0A2wm ОЛз(рис. 18.10, а),то периодический процесс с амплитудой а = а устойчив, а если по направлениям 0A,, или ОЛ - неустойчив. Это направление перемешенпя точки м = ю из начала коорди1шт с увеличением а определяется, очевидно, следующи.ми проекция.ми па координатные оси X и Y:
|