Таблица 4.1. Типовые звенья

л п/п

тип звена

передаточная функция

Позиционные

Безынсрциошюс

Апериодическое 1-го порядка

Апериодическое 2-го порядка

Колебательное

Копсерватииное

W(p) = k/\+Tp

2 2

(1 + 7зр)(1+7-,р)

W{p) =

Ч Ч

и H TO] ри py юшие

Идеальное интеджрующее

Иитсфируюн1сс с замедлением

(р) =

р(1 + 7р)

Изодромное

р V к

Идеальное дифференцируюнюе

{j))-kp

Дифференцирующие

Дифференцируюнсее с замедлением

Рис. 4.4

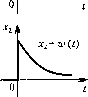Рис. 4.5

Рис. 4.6

Единичная имиу.чьсная функния или дельта-функция представляет собой производную от единичной ступенчатой функции: 5(0 = 1 (О- Дельта-функция тождественно равна нулю повсюду, Kpo.vje точки t = О, где она стремится к бесконечности.. OcHOBiroe свойство дельта-функции заключается в том, что

b{t)dt = i,

(4.3)

т. е. она и.меет единичную г1лоцадь.

Из последнего выражения следует, что размерность дельта-функции равна [с~.

Нетрудно установить связь .между переходной фу1гкцней и функцией веса. Рассмотрим входное воздействие звена в виде конечного но высоте и ширине импульса с площа,тью Ле = 1, прикладываемого при f = О (рис. 4.6). Такой и.мнульс .может быть заменен двумя ступенчатыми функциями N 1(/) и -N 1(< - е), прикладываемыми ко входу звена со сдвигом во времени е. Тогда выходная величина будет равна

X2{i) = N[h{t.)-h{t-E)].

(4.4)

Будем теперь увеличивать высоту импульса Л, одновременно умепьпшя его nni-рииу е, по так, чтобы все время плоп1адь импульса равнялась единице, т. е. Ыг = 1. По.множив и поделив правую часть равенства (4.4) иа е и перейдя к пределу, получим функцию веса

Ae.[/z(f)-/2(t-e)]

C[t) = ИП1--- =

dh{t)

J ( 5)

е dc

Таким образо.м, функция веса можетбыть нолученади(})(})еренцированием по времени переходной футсции.

В случае, если па вход звена поступает неединичная им[1ульсиая функция = G 5(г), на выходе звена получится = G ?c-(r). Импульсная ({функция также представляет собой распространенный вид входного воздействия в авто.матических системах. К такому виду.можно свести, например,

кратковременный удар нагрузки на валу двигате.чя, кратковременный ток короткого замыкания генератора, отключаемый плавкими предохранителями, и т. и. В действительности реальные импульсные воздействия на автоматическую систему всегда будут конечными по величине и И1)одолжптельности. Однако в случае если их продолжительность весьма ма-ча ио сравнению с временем переходного процесса звена и;и автомагической системы, то с большой степенью точности реальный импульс может быть заменен дельта-функцией с некоторым масп1табирующим коэффициентом, что позволяет оценить переходный процесс но виду функции веса.

Функция веса звена связана с его передаточной функцией преобразованием Лапласа, а именно: передаточная функция есть изображение фушсции веса п связана с ней нитег1)альиым преобразованием

W(p) = jw(t)e-Pdt. (4.6)

В свою очередь переходная функция звена связана с его передаточной функцией преобразованием Карсопа, т. е. имеет место иптегра;1Ьиое преобразование

W(p) = p]h(t)e- dt. (4.7)

Для входного воздействия П1)опзвольпоготипа, прикладьпшемого в .моменте = О, переходный процесс па выходе звена при нулевых пачальнььх условиях может быть определен на основании интеграла Дюамеля-Карсона до переходной функции:

X2(t) = X, (0)/г(О + Jx-, (x)h(t - x)dx, (4.8)

или по функции веса

X2(t) = jxi(T:)w(t-x)dx, (4.9)

где х -- вспомогательное время интегрирования, изменяющееся в пределах от пуля до рассматриваемого текущего момента времени t.

Более подробно методика нахождения переходного процесса при произвольном входном воздействии будет рассмотрена в главе 7.

§ 4.3. Частотная передаточная функция и частотные характеристики

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Д.я получения ее рассмотрим динамическое звено (рис. 4.1) в случае, когда во;!му1цение/(г) = О, а иа входе имеется гармоническое воздействие \ cos ш, где Х - aMOJHiTyfla, а ш - угловая частота этого во.здействия.