§ 13.5. О синтезе систем с переменными параметрами

Ввиду сложности математического решения синтез систем управления с переменными параметрами, как правило, должен осуществляться при помощи вычислительных машин непрерывного или дискретного действия, а также посредством реального моделирования. Вычислительные машины позволяют просмотреть все наиболее важные режимы работы системы, оценить ее качественные показатели и подобрать необходимые корректирующие средства.

Однако во многих случаях, особенно для квазистациопарпых систем, можно провести синтез расчетным путем. Это позволяет более сознательно подойти к определению структуры проектируемой системы и пара.метров корректирующих средств, что значительно сокращает объем последующих исследований и проверок па вычислительных мапп-гнах и моделях.

Метод замороженных коэффициентов. Одним из наиболее простых способов является замораживание переменных во времени параметров в какой-то фиксированный момент времени f = 6, что ведет к замораживанию коэффициентов дифференциального уравнения (13.1). В этом случае система с переменными параметрами сводится к системе с постоянными параметрами, что позволяет при.менять для нее известные методы синтеза (см. главу 12),

Разница но сравнению с системами, имеющими постоянные коэффициенты, заключается в том, что исследование системы с замороженными коэффициента.м и должно быть последовательно проведено для различных моментов времени t = Ь, лежащих в интервале О < 6 < Г, i-де Г - время работы системы.

Если во всем рабочем интервале времени от О до Ткачество системы управлетш оказывается приемлемым, то ее считают работоспособной и при изменении коэффициентов уравпешш в исследованных пределах.

Этот метод будет давать правильные результаты, если в течение вре.мени переходного процесса (пока функция веса не .затухнет практически до пуля) коэффициенты уравнения (13.1) успеют мало изменить свое значение.

Следует заметить, что эффективность рассматриваемого .метода может зависеть от правильного выбора фиксированных .мо.ментов времени, для которых производится замораживание коэффициентов. Необходимо так выбирать эти моменты вре-лгепи, чтобы охватить все возможные варианты значений коэффициентов, обратив особое внимание на опасные точки, в которых происходит значительное изменение коэффициента, смена его знака и т. и. Безусловно, что правильный выбор рассматриваемых моментов времени во .многом зависит от опыта проектировщика.

В качестве при.мера рассмотрим систему угловой стабилизации ракеты по yi-лу рыскания Дифференциальное уравнение ракеты как объекта управления без учета влияния воз.мущепий в простейшем случае может быть представлено в виде [93]

Ц1 + СЦ! = С2?>,

где S - угол поворота управляющих органов.

Из-за изменения скоростного напора, плотности атмосферы, выгорания топлива и под влиянием других факторов коэффициенты с, и С2 в процессе полета изменяются (рис. 13.5).

Наиболее опасными являются точки, соответствующие моментам вре.мени = f г = О, 1, 2, 3. Заморози.м в этих точках коэффициенты. Тогда в.место одного уравнения с переменными коэффициентами получим четыре уравнения с постоянными коэффициентами и, соответственно, четыре стационарных объекта.

Наиболее тяжелым с точки зрения стабилизации является .момент времени г = t когда коэффициент с, (tj) и.меет максимальное отрицательное значение. Передаточная функция объекта для этого случая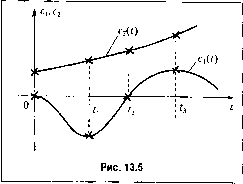

. C2(fl)

о -

Cl(l)l

в характеристическом уравнении Тр -\ = 0 имеется положительный кореш, т. е. объект статически неустойчив. Структурная схема систе.мы угловой стабилизации с таким объектом аналогична изображенной на рис. 6.5. Выберем параметры этой системы исходя из требований точности и запаса устойчивости. При необходимости введе.м в систему дополнительное корректирующее звено. Желате;1ыго, чтобы при тех же значениях параметров обеспечивалось требуемое качество системы с любым из четырех стационарных объектов. В противном случае придется производит ь коммутацию параметров или даже структуры корректирующих средств в процессе полета ракеты.

Метод замороженных реакций. Во многих случаях переменными параметрами обладает не вся систе.ма управления, а одно из ее звеньев. Чаще всего таки.м звеном оказывается объект управления. Задача синтеза будет сильно упрощена, если звено с пере.мепными параметрами исследовать отдельно, а зате.м нриближещю заменить его в окрестностях neKOTopoii точки эквивалентным звено.м с постоянными параметрами. .Задача оказывается более простой вследствие toio, что в большинстве случаев дифференциальное уравнение звена с переменны.ми параметрами может быть сведено к уравнению первого или второго порядка.

Этот метод оказывается более точным, чем метод замороженных коэффициентов, так как при замене звена с переменными нара.метра.ми эквивалентным звеном с П0СТ0Я1И1Ы.МИ нара.метра.ми учитывается факт переменности параметров исходного звена, что будет определять вид и нара.метры эквнва.лентного звена.

Идея метода заключается в следующем. Пусть и.меется некоторая система управления (рис. 13.6), содержащая в своем составе звено с переменными параметрами. Часть системы, соответствуюн1ая постоянным пара.мет-рам, выделена в отдельное .звено.

Для звена с пистояиными параметрами может быть определена весовая функция а;, (т), которая зависит то;и>ко от времещ! т t ~ д (рис. 13.1), и соотвегствующая ей 11 среда 10ч 11ая фуп кц11я

W,ip) = jw,(x)e~>dT. (1385

Для звена с неремениылт пара.метрами определим весовую функцию zf- (t - Ь, 6) = = :> (т, 0). Эта весовая функция можетбыть найдена точно, если дифференциальное уравнение звена и.меет первый или второй порядок или приближеппы.ми .методами в соответствии с изложенным в § 13.2 и § 13.3. Для ее 1гахождеш1я могут быть также использованы вычислите;И)11ые машины с последуюп1ей аппрокси.мацией решения.

Посте нахождения весовой (1эу1П<пии ffj заморозим ее для некоторого фиксиро-Bainioro мо.мента времени t = -Qq, по;1агая при это.м, что весовая функция па небольшом иптервате времешг вблизи точки = -Oq зависит только от времени т = т - 6 и не зависит от зафиксированного значения смещения. Таки.м образом, мы получи.м функшпо

1£2(1--д,х%)-г02(т,-до). (1.3.86)

Заметим при это.м, что мы фиксируем аргумент f) не полностью, а только в той его части, которая делает рельеф функции веса нецилнндрическим. В ре.зультате этого оба разреза (рис. 13,2) получаются одинаковыми, т. е. весовые функции (13.5) и (13.7) совпадают.

Для весовой фугпсшн! (13.98) .может бьпь найдена передаточная функция

Щ(Р,\) = ]Щ(-\)( dx. (13.87)

Эта передаточная функция по своей суниюсти является нараметрической, так как в нее входит фиксированный нара.метр Ь. Однако 1Ю своим свойства.м она полностью совпадает с передаточной функцией звена с 1Юстояипыми параметрами. Вследствие этого будем называть ее эквивалентной иередаточной функцией. С OToii передаточной футсцисй можно в дальпейше.м оперировать так, как будто рассматривается звено с постоянными параметрами. В связи с этим рассматриваемую передаточную ([пункцию .можно записать сокращешю: IV iP о) ° 2 (Р)-

Однако при это.м надо no.vnniTb, что исследовашю систе.мы должно быть произведено при различных значениях фиксированного параметра в пределах О < < Т.

Д;1Я системы, изображешюй на рис. 13.6, при использовании эквивалентной передаточной функции может бьггь найдена передаточная функция разо.\и<нутой системы

W{i))-W,{p)W2{p), (13.88)

передаточная фушсция за.мкнутой системы

\ + \Vip) \ + W,ip)W2(p)