й, причем паиравлепие касательной MjVопределяется вектором с проекциями (18.62). Это геометрическое условие устойчивости периодического решепия можно записать в следующем аналитическом виде:

.да)

(дГ\ Эй)

>0,

(18.63)

или иначе:

ЭХ Э£ЭХ Э dq да dq да

ЭУ Эо)

ЭУ ЭЭУ Э£ dq да dq да

Uo)

>0.

Здесь важно, что частные производные берутся не по частоте о), а по текущему пара.метру кривой Михайлова м, т. е. имеются в виду выражения Хи Уне в форме (18.35), а как вещественггая и мнимая части выражения (18.45) в функции от (Ьщт ю = const (если она входит в ко:ф4)ицие1Гты, стоящие в квадратных скобках этого выражения).

Выполнение условия (18.63) устойчивости периодического реигепия во всякой конкретной :!адаче можно проверить аналитически, без построения кривых. Этого достаточно для систем третьего и четвертого поря/н<:ов, если все коэ()фициепты гармонически линеаризованного характеристического уравнения иоложитсльпы. Для систем же пятого и более высокого ггорядков требуется догголпительно проверить общий ход кривой Михайлова, чтобы убедиться, что и.меет .чгесто случай, например, рис. 18.11, а, гю не рис. 18.11, б. ,3амети.м, что в.место построения кривой Михайлова можно и тут воспользоваться анагитическим догголнительпым условием, потребовав выполнения критерия Гурвица для .мпо1-очлепа

/),<Р)-4Ц-.

9 У

(18.64)

где D (р) - левая часть гармонически линеаризованного характеристического урашю-пия (18.33) при а =а,Иа) = ю , при этом если D(p) имеет пятую или шестую степень,

достаточью убедиться в положительности коэффициентов (р).

Устойчивость равновесного состояния системы. Приведенгп>1е в нача-че данного параграфа гармонически линеаризованные уравнения нелиней-гюй системы годятся только для колебательных процессов, определяемых нериодически.ми решениями, и для колебательных переходных процессов в иепосредствешюй близости от указанных периодических регггепий. Поэтому, строго говоря, с помощью этих приближенных уравнений .можно анализировать только сами перио/пщес-кие решения и их устойчивость или неустойчи-

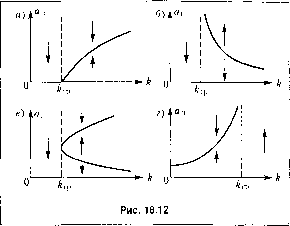воеть при малых оттстопениях от исследуемого колебательного режима, что выше и делалось.

Практически лее из анализа полученных приближенных уравнений пелипейпой системы часто можно делать значительно более широкие выводы. В частности, можно оценивать устойчивость системы в тех областях ее параметров, в которых периодические решения отсу гствуют вовсе.

Пусть, например, определено, что периодическое решение, амплитуда которого показана па рис. 18..5, а, устойчиво (оно соответствует автоколебания.м). Условимся факт устойчивости периодического решения обозначать па графике вертикальными стрелками, сходянптмися к данному периодическому реп1епию (рис. 18.12, а). Этим обозначением иллюстрируется то, что переходные процессы с обеих сторон (г. е. с больпнт.ми, чем а , и с меньпшми, че.м а , начальными амилитуда\п1) сходятся к автоколебательно.му процессу с амплитудой а . Пусть в данном случае к обозначает коэффициент передачи линейгюй части. График рис. 18.12, а показывает, что в системе возникают автоколебания при к > к.. Естественно сделать отсюда вывод о том, что в области О < Л < .р (где нет периодического ренгения) данная система будет устойчива, что также обозначено на рис. 18.12, а вертикальной стрелкой.

Апачогичное заключение для области О < й < .р .можно сделать и в случае неустойчивого периодического репюния па рис. 18.12, б, и в случае па.;и1чия двух периодических решепий на рис. 18.12, о, одно из которых устойчиво, другое неустойчиво. Если же автоколебания наблюдаются в области О < к < к., как показано па рис. 18.12, г, то естественно предио.чожить, что область к > к.. будет областью неустойчивости данной нелинейной системы.

Наконец, если периодических решепий для исследуемой нелинейной систе.мы ffc получается вовсе ни при каких згшчепиях ее параметров, то согласно гео.метрическому способу определения автоколебаний (см. выше) получим, что кривая Михайлова будет либо охватывать начало координат при всяком значении а, либо ие охватывать его ири всех а. Отсюда можно сделать вывод, что в перво.м случае данная нелинейная система устойчива, а во втором - неустойчива.

Развитие, а также сравнение да1шого способа определения устойчивости равновесия не.тинейиой системы с методом Ляпунова, показьшаюшее эффективность такого способа, см. в книге [72, §§ 2.7-2.9].

§ 18.3. Примеры исследования нелинейных систем первого класса

Рассмотрим несколько примеров применения изложенного в предыдущем параграфе метода.

П р и .м е р 1. Найдем влияние ограничения лиггсйной характеристики двигателя (рис. 18.13, а) па процессы в следящей систе.ме. Пусть остальные звенья системы ли-пейр1ы. Тогда уравнение управляемого объекта с двигателем вместо (16.63) примет вид

(r p+l)pP-cf(U,

\j\eF{i) определяется графико.м рис. 18.13, а.

Применяя к правой части этого уравнения формулы гармонической линеаризации (18.22) с заменой с = 6 получаем уравнение управляемого объекта с двигателем в виде

(г /;+1)рР = ./( )/ ,

q = k, =ck.

. b b arcsm -+ - . a a\

при a < b, при a>b.

(18.65)

(18.66)

что изображено графически на рис. 18.13, б. Здесь а обозначает амплитуду колебаний величины zj,.

Общее уравнение остальной части следящей системы согласно (16.53) будет

(Г,р+ l)i, = -f+ (/>+ 1)0/IP- (18.67)

На основании (18.65) и (18.66) 1голучаем характеристическое уравнение

(Г р + 1) (Г р +\)p + q {а) [к + (Г я + \)к,р\ = 0. (18.68)

После приведения его левой части к виду flgp + ajp -t aj) + a.-j и подстановки p =j(X) получаем уравнения типа (18.36) в виде

X = kq(a ) - [/; + Г + Т кд(а )\и>1 = О, y = (l-r/V/( )K-/;?; n=0.

(18.69)

Выясни.м влияние параметра к на автоколебания в данной системе. Из последнего уравиепия находим

,(a ) = i;M,

(18.70)