Эквивачситная передаточная функция замкнутой системы с учетом дополнительного канала

IV(2)

E{z)

ф Цо(2ЯО(2) + £(2)] 1 D{z)

1 + 0(2)\Уо(2) \ + \V{z) 1 + 1V,(2)

(15.27)

где W{z) = D{z) Wq{z) - передаточная функция разомкнутой системы; IV (2) - эквивалентная передаточная функция разомкнутой системы. Эквивалентная передаточная функния но ошибке

Ф. (2)=1-Ф.,(2)=ьв£Ж£):

1 + Щ2)

Эквивалентная передаточная 4)ункция разомкнутой системы

.(,ч Ф:>() lVo(2)[Z)(z) + £(2)]

1-Ф,(2) \-E{z)W,{z)

(15.28)

(15.29)

Из формулы (15.28), если положить Ф (2) О, можно получить условие полной инвариантности

1 Я,(2)

Е{2) =

lVo(2) E,{z)

(15.30)

Для больнитнства реальных систем степень числителя IVq(2) оказывается меньше степени зна.менателя на единицу. Поэтому степень полинома £,(2) будет на единицу больше степени полинома £2(2) и формула (15.30) может быть приве;дена к виду

£(2) = C2+-ii--

Aq +Я,2 +... + а2

(15.31)

Слагаемое cz = сеозначает, что при формировании сигна;ш по каналу с передаточной функцией E{z) необходимо использовать упрежденное 1ш одни такт значение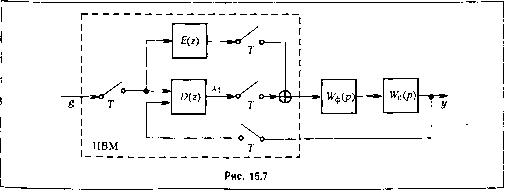

задающего воздействия. Это связано с необходимостью применения прямых разностей, которые в дискретном плане должны здесь заменить иропесс дифференцирования (см. § 14.2). При зтом возможны следуюпите ситуации.

1. Если ЦВМ вычисляет значение задающего воздействия но некоторым заложенным в нее данным и использует при этом прогнозирование (например, при вычислении текуи[их координат небесных тел, спутников, ракет и др.), то вычисление будуптего значения интересующей ве;птииы может быть легко сделано со сдвигом па практически любое число тактов. В этом случае реализация формулы (15.31) в принципе возможна. Однако практические трудности в])еа;1изации слииисом сложных а;и орит.мов и ограничения в.элементах ие дают возможности получить полную инвариантность.

2. Если ЦВМ вычисляет задающее воздейсгвие не по принципу нрогнозированпя, а в результате обработки поступающей текущей информацип, то точная реализация формулы (15.31) оказывается невозможной. Тогда приходится ограничиться прибли-же1июй реализацией формулы (15.30) либо вводить в прямой канал дополиительное запаздывание па один такт. В нервом случае условие полной инвариантности (15.30) парущается, во второ.м - вводттгся носгояпное временное запаздывание иа один такт к обработку задаюнтего воздействия, что также на1)ушает условие инвариантности.

Таким образом, при использовапни комбинированного управлетиш приходится ориентироваться не иа полную инвариа1ГГность, а па некоторое, во .многих случаях весьма существепиое, повышение точпостть

Поскольку точность систем управлепия определяется низкочастотно! ! частью л, а. x., а низкочастотная часть л. а. х. лискрет!!ь!х chctcn! г!рактическт! сливается сл. а, х. непрерывной части системы, то расчет дпскретн111Х систе.м !со.мби!)ировап!)01-оу!1рав-ле1!ия осу1![ествляется аналогично Ь!е!!рерыв!Тому случаю 9].

Важ!1ейи!и\! следствием ис!!ользоваиия комбииирова!И1огоу!!равле!!пя я!!ляется воз\!Ожностьснижения требовант!Й к ЦВМ в части огра1и!че!!ия периодаЛ1!скрет!!0с-ти. Это связано с !!онижепием требований к кана;1у унравле1!пя по ог!<ло!!ению при введении до!!олните;!ь!!ого канала с !!ередаточиой фу!!!ии!ей E{z).

§ 15.3. О синтезе систем управления с ЦВМ

Синтез систем управления с ЦВМ па!1более iipocTo производить i!a основе той методики, которая б!)1ла изложе!1а в § 12.6 для т!епрерывпь!Х систе.м. Покажем, !<ак можно !!ере!!ести ее на дискрет1!Ые систем!)! управления.

Как и в случае непрерывных систем, будем 0!1ределять !<ачество 1!ереходпо!-о процесса устойчив!>1х дискреТ!И)!Х систем, точ1!ее их запас устойчивости, i!0 показателю ко.мебательиости, соответствующему максиму.му амплитудной частот!1ой хара!сгернс-тики замкнутой системы:

М=\ф{]Х)\

W{jX)

i + W{jX)

(15..32)

Соотпо1пение( 15.32) Г!олт!остью а!1ало!Т1Ч!!о соответствующему сооттк)!иеппюД.1Я ненрерывнь!Х систем. Поэтому получение т1)ебуемого показателя колебательности мо-жетб!)1ть обеспечено В1)!ИолнеИ!1ем условия для л. а, х. разомк!!утой С1!стем!)1 подоб!то тому, !<ак это было сделано в § 12.6для !!е!!рерывнЬ!Х систем.

Для упрощения выкладок ограничимся рассмотрением систем с астатизмом ие выпте второго порядка при наличии двух непрерывных интеграторов, хотя методика остается применимой и в случае более высокого порядка астатизма. Пусть передаточная функция иенрерывной части разомкнутой систе.мы имеет вид

При построении л. а. х. следяп1ей системы с учетом ЦВМ введе.м следующие ггред-положепия.

1. Величина, обратная периоду дискрстпости 7, больше половины частоты среза (0, л. а. X. непрерывной части системы, т. е. а)(.рГ.< 2. При расчете следящих систем с ЦВМ .это неравенство приходится выполнять практически во всех случаях в связи с гребо-вапиями по устойчивости и запасу устойчивости.

2. Все постоянные времеш! 7 , . . ., Г можно разделить на две группы. К первой фунпеГ ..., отнесем тс из них, которы.м соответствуют сопрягающие частоты, меньшие частоты среза а),., (большие постоянные времени). Ко второй группе Г...., Г отпесе.м те постоянные времени, которым соответствуют сопрягающие частоты большие, чем частота среза (ор (малые постоянные времени), причем для каждой постоянной времени второй группы должно выполняться неравенство 7 ,< 772.

3. Постоянным временем Tj,..., т соответствуют сопрягающие частоты меньпте, че.м частота среза. Это пе относится к те.м постоянным времени числителя передаточной функции разо.мкнутой непрерывной части, которые были введены для компенсации некоторых ее полюсов и поэтому после сокран1еиия соответствующих мпожите-.чей ие вошли в окончательное выражение (15.33).

4. Переход оси нуля дешгбел асимптотической л. а. х. пеирерывиой части нронсхо-дит ири отрицательно.м наклоне 20 дБ/дек.

Л. а. X. системы с ЦВМ в области низких частот. Рассмотри.м тюстросиие л. а. х. для (15.33) в области низких частот, т. е. левее частоты среза. Передаточная функция пе-пр.ерывной части для этой области может быть представлеиа в виде

u7 .( + lP)--( + mP)

р (1 + Г,р)...(1 + / Я)

Очевидно, что вследствие условия 4 имеем равенство m = q+ \ . Разложи.м (15.34) на простые дроби;

Шр) = ~К±-, (15.35)

р р ыЛ+Ър

где Л,. - коэффициенты разложения. Я ? = Kq представляет собой условную добротность по скорости, а

т <1

То-Ък-и-г (15.36)