366 Непрерывные линейные системы автоматического управления Тогда вместо (12.56) можно записать

л Атах Yl/lO

-max + (12,60)

Отсюда находим требуемое значение коэффициента передачи:

К = + У. (12.61)

o,fax Ощах

В системах стабилизации ошибка определяется только наличием возмущения (или возмущений). В этом случае требование к низкочастотной части л. а. х. сводится к необходимости иметь определенное значение коэффициента передачи разомкнутой системы, вне зависимости от того, является ли система по виду передаточной функции W(p) статической или астатической.

Это значение коэффициента передачи будет определяться вторым слагаемым в правой части (12.61) или су.ммой подобных слагаемых при действии нескольких возмущений. По коэффициенту передачи может быть построена первая асимптота желаемой л. а. x.

Требования к запасу устойчивости. В следян1их системах повышение коэффициента передачи разомкнутой системы вызывает приближение к колебательной границе устойчивости. Это проявляется в увеличении колебательности системы. Для оценки запаса устойчивости, т.е. степени удаления от колебательной границы устойчивости, могут использоваться различные критерии, в том числе такие, как, например, перерегулирование при единичном входно.м возмущении, запас устойчивости по амплитуде и по фазе и т.н.

При использовании частотных критериев качества наиболее удобно оценивать запас устойчивости замкнутой системы по показателю колебатетьности М, который характеризует склонность системы к колебаниям (см. гл. 8).

В астатических системах для за.мкпутой системы коэффициент передачи на нулевой частоте равен единице. Поэтому под показателем колебательности пони.мается абсолютное значение наибольшего максиму.ма

М = Ф(;а))

W(jm)

Это положение остается справедливым и для статических систем, так как для исключения статической ошибки по задающему воздействию в них, как правило, используется .масштабирование выходной величины посредством применения неединичной обратной связи (см. § 9.3) с коэффициентом к< \. Тогда коэффициент передачи замкнутой системы на нулевой частоте может быть сделан равным единице соответствующим выбором величины k,:

Ф(,о)= (0) .-=1,

где К - коэффициент передачи разомкнутой систе.мы.

Показатель колебательности Л/ = 1,1 н- 1,3 соответствует очень хороншму демпфированию системы, при котором перерегулирования весьма малы. Показатель колебательности М = 1,3 1,5 обычно является вполне достаточным для больпшпства следящих систе.м. Во многих случаях следящие системы работают удовлетворительно и при значениях М = 1,6 1,8.

Необходимым и достаточным условием того, чтобы в устойчивой системе показатель колебательности был не больше заданного, является нахождение фазовой характеристики вне запретной зоны (рис. 8.21). В минимально-фазовых системах это условие может быть выдержано соблюдением определенных правил построения л. а. x. без нахождения фазовой характеристики.

Рассмотрим принципы построения л. а. х. с заданным показателем колебательности. По методически.м соображениям рассмотрение начнем со следящих систе.м с астатиз.мом второго порядка, хотя эти системы и ие относятся к наиболее иросты.м и распространепным.

Как правило, в качестве типовых используются л. а. х и.меюпше в низкочастотной части наклон не более -40 дБ/дек. Это вызвано стремлением избавиться от условий, при которых возможно появление неустойчивости в большо.м, т. е, ири согласовании следящей системы с большого угла.

Типовые л. а. X. систем с астатизмом второго порядка. В системах с астатизмом второго порядка обычно имеются два интегрирующих звена. Такими звенья.ми могут быть исполнительный и вспомогательный двигатели, например гидромуфта и управляющий двигатель, поворачивающий шпиндель или чапгу гидронасоса. В некоторых случаях астатизм второго порядка может появляться вследствие особенностей механических характеристик единственного исполнительного двигателя, у которого вращаюпшй момент не зависит от скорости вращения.

Рассмотрим передаточную функцию разомкнутой системы вида

v,(p)=M!lZk).

(12.62)

где [с~] - коэффициент передачи по разомкнутой системы, называемый добротностью по ускорению.

Асимптотическая л. а. х., соответствующая (12.62), и.зображена па рис. 12.10, В соответствии с наклона.ми асимптот, кратными -20 дБ/дек, ей присвоен тип 2-1-2.

Отсюда находится требуемое значение коэффициента обратной связи;

-iso.o-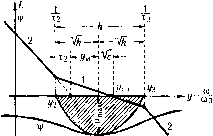

Рис, 12.11

Положение всей л. а. х. может быть задано точкой пересечения первой асимптоты с осью пуля децибел. Этой точке соответствует частота

(12.03)

которую назовем базовой.

При введении новой переменной q =p/(Oq передаточная функция будет представлена в нормированном виде:

(12.64)

где Tj = и Т3 = а)()7з - относительные постоянные времени.

Соответствующая пор.мированпая л. а. х., построепная для относительной частоты у = co/cOq, изображена па рис. 12.11. Здесь же показаны для иллюстрации фа.зовая характеристика и запретная область для нее.

Протяженность участка с единичным наклоном, т. е. с отрицательным наклоном 20 дБ/дек, определяется отнощением двух постоянных времени (см. § 8.8 и рис. 8.25):

/3 3

(12.65)

Под протяженностью участка вдоль оси частот (рис. 12.11) понимается отношение частот конечных точек участка (бо;1ьшей к меньшей). Запас по фазе для функции (12.64)

ц = arctg г/Т2 - arctg г/Тз = arctg

i + hyhj

(12.66)

Исследование па .макси.мум дает

1тах= arctg

T3VA

Isfh

(12,67) (12.68)

Максимальный запас по фазе определяется только протяженность асимптоты

л. а. x., имеющей единичный накло1Г

Приравнивание максимальных запасов по фазе (8.88) и (12.68) дает зависимость

между протяженностью участка h и показателем колебательности Мпри онтималь-