окончательно получаем

fit) = -

С05ф---р

(21.4)

Подставив это выражение в заданное дифференциальное уравнение системы (21.2), получим

Qkp)-S{p)

СОКф---р

x + R(p)F(x,px) = 0.

(21.5)

Таким образом, неоднородное нелинейное уравнение (21.2) при задатюм внешнем воздействии (21.1) и предполагаемой форме решении (21.3) сведено к однородпо-.му нелииейно.му уравнению (21.5), содержащему добавочный член в левой части. Уравнепие (21.5) аналогично прежнему уравнению (§ 18.2) и отличается от него только заменой (шераторного многочлена Q (р) на новый операторный м1югочлен, стоянщй в (21.5) в квадратных скобках. Применяя нри отыскании синусоидального периодического решения формально тот же .метод, что и в главе 18, нужно потребовать вьпюлне-пия свойства фильтра от этой новой системы.

Заданная нелинейность f(x, рх) должна допускать симметричные колеба1Н1я, т. е. должно выполняться условие

jf(flg.sinv, u! a) cos\/)(i\/ = 0.

(21.6)

Итак, получив для определения вынужде1Н1ых колебаний однородное уравнение (21.5), можно, как и в § 18.2, произвести гар.моническую линеаризацию пелипейности

F(x, px) = qx +-рх,

О),.

(21.7)

ЛЯ 1

F(a sin\/, й со cos\/)sin\/ir/\/,

F(a sin\/, fl to cos\)j)cos\/J\;,

Ii о

(21.8)

причем согласно (21.3)

V == -t- ф.

(21.9)

что, однако, пе влияет на результат вычисления q и q. Поэто.му при определении симметричных однозначных вынужденных колебашн ! можно целиком пользоваться гого-

выми выражениями для q и q. приведеииыми в главе 18, с заменой в них а, со иа а , со . Таким образом, для каждой нелинейности в общем случае получаются зависимости

q (я, (0 ), q (о ), а во .многих частных случаях (см. главу 18) -

q (а ), (7, (а ).

(21.10)

(21.11)

В результате из (21 .,5) и (21.7) нолучае.м характеристическое уравнение для первого приближения

Q(p)-5(p)-

со.чф---р

+ R{p)

q + --p

= 0.

(21.12)

Подставляя сюда чисто мпи.мое значение р = Уо) , что соответствует отысканию синусоидального решения (21.3), получаем

QCA) - (М,)-(ссхчф - ysin ф) + R{j(x\ )(q + jq) = 0. (21.13)

-iif

Замечая, что

С03ф-7 31пф = <?

из уравтюния (21.13) находим, что

Я7Ч)

Воз.можны два метода дальнейшего реп1еиия задачи. Эти методы остаются справедливыми и для нелинейных систем с вре.менным запаздыванием т, когда выражение (21.14) принимает вид

(21.14)

5(;4)

(21.15)

или другой аналогичный вид, содержапнш т.

Графический метод. Для каждого значения частоты ири заданных параметрах систе.мы на комплексной плоскости строится кривая (рис. 21.1)

/(а ) = а Q04) + O..)(/+7V) .9(70) )

(21.16)

.Эта кривая ссютветствует левой части равенства (21.14). 11равая же часть (21.14) изобразится в виде окружности радиуса В. Пересечение ее с кривой Z(ag) дает ркмпе-пие задачи, приче.м в точке пересечения но дуге окружности определяется фазовый сдвиг ф, а но кривой Z (а ) - величина амплитуды а вынужденных колебаний.

Лиалогичмо решается з.1дача и н случае выражения (21.15).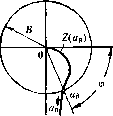

2(ав);

При ралпых сОй или k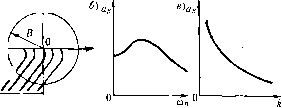

Рис. 21,1

Рис. 21.2

Зависимость амплитуды вынужденных колебатш от частоты а) (рис. 21.2, б) можно получить, если нарис, 21.1 начертить серию кривых Z(a ) при разных постоянных значениях (рис, 21.2, а). Таким же путем, строя кривые Z(aB) при разных постоянных значениях какого-нибудь пара.метра k (рис. 21.2, а), можно определить зависимость йв от любого параметра системы k (рис. 21.2, в), входящего в выражение (21.16) для Z(aJ.

Для отыскания зависимости а от амплитуды внешнего воздействия В нужно нанести серию концентрических окружностей разных радиусов В (рис. 21.3, а). При этом возможны два случая: 1) когда имеется точка пересечения окружности с кривой Z(a ) при любой величине радиуса В, начиная от нуля, что дает зависимость (В), например, в виде рис. 21.3, б; 2) когда точка пересечения окружности с кривой 2(0) существует только при зпачепиях радиуса В, превышающих некоторое пороговое значение й р (рис. 21.3, а), что приводит к зависимости а (В) типа рис. 21.3, е.

Графическое определение 5 р ясно из чертежа. Можно построить зависимость пороговой амплитуды В , р внешнего воздействия от частоты а) нри заданных параметрах системы (рис. 21.3, г) или от любого параметра k при данной частоте (а (рис, 21.3, д). Последнюю зависимость можно найти с помощью рис. 21.3, а, построенного для серии кривых Z (fifg), соответствующих различным k.

Рассмотренный второй случай, когда система перехо-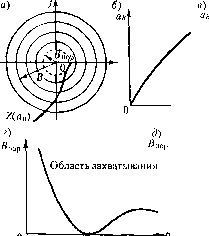

й О в,

Область захватывания

(йаит

Область Область авто- устойчивости колебаний равновесия