В соответствии с формулой теоремы запаздывания для изображений 4)ункций но Лапласу для элемента чистого запаздывания получаем передаточную функцию в виде

Wi]))-e. (6.35)

За.метим, что в некоторых случаях наличие большого числа малых постоянных времени в систе.ме управления можно учесть в виде постоянного запаздывания, равного су.м.ме этих постоянных времени. Действительно, пусть система содержит jVпоследовательно включенных апериодических звеньев первого порядка с коэффициентом передачи, равны.м единице, и величиной каждой постоянной вре.мени Тогда резу;1ьтнрующая передаточная функция будет

f г

{\+TpУ

(6.36)

Если N-oo, то в пределе получаем W(p) = е~. Уже при ,V = 8 + 10 передаточная функ1П1Я (6.36) .мало отличается от передаточной функции .звена с запаздыванн-ем (6.35).

Уравнение любого линейного звена с запаздыванием (6.33) будем теперь записывать в виде

С(р)х, = 5(р)е- х,. (6.37)

Передаточная функция линейного звена с заназдьшаинем будет

W{p) = e-> = WQ{py-- .

(6.38)

где через Wip) обозначена передаточная функция соответствующего обыкновенного звена без заназдывагигя.

Частотная передаточная функция получается из (6.38) подстановкой р = jw.

(6.39)

гдеЛо((о) и V()(co) - модуль п фаза частотной передаточной функции звена без запаздывания.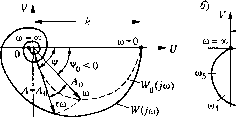

(0=0

Отсюда получаем следующее правило.

Для построения амплитудно-фазовой характеристики любого звена с запаздыванием нужно взять характе})истику соответствующего обыкновенного звеиа и каждую ее точку сдвинуть вдоль ок[)ужности по часовой стрелке на угол тю, где со -значение частоты колебаний в дайной точке характеристики (рис. 6.23, а).

Так как в начале амплитудно-фазовой ха[)актеристики со = О, а в Koinie (О = оо, то иача7И>ная точка остается без изменения, а конец характеристики аси.мптотически навивается на начало координат (если степень операторного многочлена В меньше, чем м1К)Гочлена С).

Выше говорилось о том, что реальные переходшяе процессы (временные характеристики) вида рис. 6.22, б часто .могут быть с одинаковой степенью приближения описаны как уравнением (6.31), так и (6.34). Амплитудно-фазовые характеристики для уравнений (6.31) и (6.34) показаШ)! на рис. 6.23, а и б соответственно. Принципиальное отличие первой состоит в том, что она и.меет точку D пересечения с осью U. При с[)авиеиии обеих характеристик .между собой и с экспери.мепталыюй амилитуд-1К)-фазовой характеристикой реального звена надо принимать во внимание ие только фор.му кривой, по и характер распределе1н-1я от.меток частот ш вдоль нее.

Д;ш систе.м авто.матического управления, и.меюпп1Х в числе своих звеньев одно звено с запаздыванием, все выведенные в главе 5 обирге формулы для уравнений и передаточных функций остаются в силе, если в luix подставить значения иередаточ-}и>1х фу1и<:ций в виде (6.38). Тогда передаточная функция разомкнутой системы с запаздыванием будет такой же, как (6.38), но теперь Wf{p) - передаточ1шя функция разо.мкнутой системы без запаздывания.

Характеристическое уравнение замкнутой системы, как показано в гл. 5, имеет вид

D(p) = С(р) + В(р) е-Р = 0. (6.40)

Для ycT0ii4HB0CTn системы необходи.мо и достаточно, чтобы все корни т[)ансцеи-дентпого характеристического уравнения (6.40) имели отрицательные веп;ественные части. По в отличие от обыкнове1Н1ого алгебраического уравнения здесь вследствие 1ШЛИЧИЯ множителя е~ уравнение может иметь бесконечное количество коршгй.

К указа}П1ым системам применим крите[)ий устойчивости Найквиста в его прежней формулировке (см. главу 6). Однако здесь вследствие наличия множителя е существенно изменяется очертание а.мплитудно-фазовой характеристики разомкнутой цени, построенной ио частотной передаточной функции

причем размыкание системы п[)Оизводится по определепно.му правилу, которое дается ниже

Как следствие, для устойчивости линейных систем первого и второго порядка с запаздыванием, оказывается, уже недостаточно только положительности коэффициентов, а для систем третьего и более высокого порядка с запа.здывание.м неприменимы критерии устойчивости Вышпеградского, Рауса и Гурвица.

Ниже будет рассмотрено определение устойчивости только по к[)итерию Найквиста, так как его использование для этой пели оказывается наиболее простым.

Т1-Гй

Рис. 6.24

Построение амилитудпо-фазовой характеристики и исследование устойчивости по критерию Найквиста лучше всего производить, если передаточная функция разомкнутой систе.мы представлена в виде (6.38). Для получения этого необходимо произвести соответствующим образо.м размыкание систе.мы.

Для случая, изображенного па рис. 6.24, а, размыкание можно сделать в любом месте главной цепи, например так, как это показано. Тогда передагочпая функция разомкнутой системы будет

W(p) = W,(p)

+ Щ(р)Шр)

Щ(р1

что совпадает по форме с (6.41).

Для слутая, и.зображенпого на рис. 6,24, б, размыкание главной цепи дает выражение передаточной функции разо.мкнутой системы, неудобное для дальнейших исследований:

W{p) = W,{p)

Wip)

\ + W;{p)W.,(p)e

в этом случае удобнее разо.мкпуть систему по цепи .местной обратной связи. Тогда передаточная функ1Щя разомкнутой системы приобретает вид, совпадающий с (6.41):

Щр) = -

щ(р)

Ж(р)е

l + W2(p)W,(p)W,{p)

Наконец, в случае, изображенном па рис. 6.24, в, при раз.мыкании систе.мы в указанном месте получаем выражение, также совпадающее с (6.41):

\ + W,(p)W,{p)W2(p) Частотную передаточную функцию (6.41) .можно представить в виде

W(j(i>) = Wo(j(i))e-j . (6.42)

Кро.ме того,

1Уо(;м) = А)( )е \ (6.43)

где Ло(со) - .модуль и Цо(ш) - фаза (аргу.мепт) систе.мы без запаздывания. Модуль второго сомножителя (6.43) равен единице, а его аргумент рдвен А\]1 = шт. Поэто.му, представив выражение (6.41) в виде

Щ;со) = Л(ы)е>( >,