лит на одночастотныс колебания с частотой со только ири В > й ур, наблюдается чаихе всего в таких нелинейных системах, которые до приложения внешнего периодического воздействия работают в автоколебательном режиме. При этом величина B, обращается в нуль в то.м случае, когда частота со совпадает с частотой автоколебаний со данной системы (рис. 21.3, г). й р равно нулю обычно также в области отсутствия автоколебаний (область устойчивости равновесия системы, рис. 21.3, д).

Тогда выше кривых па рис. 21.3, г, с) будут лежать значения амплитуды В внешнего воздействия, при которых суп1;ествуст одночастотный режим вынужденных колебаний с частотой со,з (область захватывания), а при значениях, лежащих ниже криво!!, будет и.меть место более сложное вынужденное движение системы. Это и является определением (пока графическим) условий захватывания, о которых говорилось выше.

В других нелинейных систе.мах может быть В о, = О, как в случае рис. 21.3, б.

Аналитический метод, Из равенства (21.14) или (21.15) можно получить аналитические выражения для определения амплитуды а и сдвига (})азы ф одночастотных вынужденных колебаний нелинейной системы. Для этого выделим вещественные и мни.мые части числителя и знаменателя и запишем равенства для модулей и аргументов обеих частей уравнения (21.14) или (21.15):

,Х(. ,coJ.F(.,.,coJ., , Х(со,) + у2(со )

Ф = -агсГйДМ.агсС8-М, (21.18)

X(a ,coJ 5(4)

гдеХи У - вещественная и мнимая части числителя выражения (21.14) или (21.15); X.,-и Уу- вещественная и мнимая части знаменателя, т. е. 5(/Шв). При этом X и Усоответ-ствуют левой части заданного нелинейного уравнения (21.2), т. е. являются теми жс самыми выражепняхпгХи У, которые применялись при исследовании автоколебаний (§ 18.2), а Ху и Уу являются новыми выражениями, соответствуюнпгми правой части заданного нелинейного уравнения (21.2).

Как видим, выражение (21.17) может, Boo6nie говоря, оказаться довольно сложным алгебраически.м уравнением относительно а . Однако важно то, что это уравнение содержит липн> одну неизвестную а , которая, следовательно, так или иначе может быть определена. После этого фазовый сдвиг ф легко вычисляется но фор.муле (21.18). Напомним, что и при отыскании автоколебаний (глава 18) часто получалось сложное относительно а уравнение, но это не вызывало больпшх .затруднений. Действительно, в большинстве случаев интересуются тем, как будет изменяться амплитуда вынужденных колебаний в зависимости от частоты и амплитуды внептего во:!действия, а также при изменении того или иного параметра системы. Указанные параметры могут входить в уравнение (21,17) более простым образом, чем амплитуда а . Тогда уравнение (21.17) можно будет разрепигть в явном виде относительно любого из этихч1ара-метров, а зате.м, задаваясь разны.ми значениями а и вычисляя но найденной фор.муле рассматриваемый параметр, можно построить искомые зависимости а (В), а (со ) или а (k) и т. п.; затем по фор.муле (21.18) можно также вычислить для каждого случая фазовый сдвиг ф.

-М (а)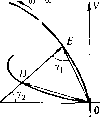

Рис. 21,4

Рис. 21.5

Например, возможен следующий простой прием решения уравнения (21.17). Для каждой заданной частоты внепшего во.здействия ш буде.м задаваться разными зпачепия.ми а и вычислять каждый раз величину В. По результатам этих вычислений легко строится график (рнс. 21.4), который и представляет собой искомое решение уравиепия (21.17).

Что касается условия захватывать, то оно .может быть опре.телепо аналитически как условие суп1ествоваиия вещественного положительного решения для в уравнении (21.17). Это условие автоматически выявится при построении графика типа рис. 21.4.

Итак, получены амплитуда и сдвиг фазы ф вынужденных колебаний для пере-мешюй X, стояп1ей под знаком нелинейной фут<ции. После этого .\и)Жпо подсчитать амплитуду и фазу первой гар.моники вынужденных колебагтй для любой другой переменной исследуемой системы на основании соответствуюиптх уравнений пли передаточных функций звеньев, связываюнщх эту переменную с переменной х.

Частотный метод. Пусть нелинейное звено в систе.ме онределяется уравнением

y = F{x).

(21.19)

Находи.м для пего прибчиженную амплитудно-фазовую характеристику W(a) согласно фор.мулам (18,210) и (18.211). Рассмотри.м два случая.

Первый с л у ч а й. Передаточная функция х , замкнутой сисгемы такова, что

X 1 М.,(/ш)

- - (21.20)

/ i + W AJ(xmXa) M,(7W) + VK (G)

- обратная а.\шлитудпо-фазовая характеристика линейгюй части.

гдеМлОа))= . л(7 )

Изобразим характеристики (jm) и -U (а) на комплексной н.тоскосги (рис. 21.5).

Амплитуда a вынужденных колебаний величины хопределяет точку Д а час гота шуточку е. Из формулы (21.20) и из чертежа (рис. 21.5) находим

.1 (7Шв)

M,(jmJ + W,(a) DE

откуда амплитуда В виептего периодического воздействия/получает значепие

й = - п- (21.21)

Переметая точку D вдоль кривой ~ W (а), можно найти зависимость величи иы я от в при заданной частоте со , а перемещая точку Е - завнси.мость величин1> а от частоты со .

Второй с л у ч а й. Передаточная функция x/f замкнутой системы такова, что х \У,и(л) 1

/ l + W,(jco)W (fl) M,Oco) + U/ ( ) 2-22)

. Тогда иа осповапии этой формулы и чертежа (рис. 21.5) получаем

fl 1 1

откуда

M,(yco) + lV ( ) DE

BDEuf,. (21.23)

В других случаях, когда передаточная с)ункция не подходит под частные виды (21.20) и (21.22), [юстроения усложняются.

§ 21.2. Несимметричные вынужденные колебания с медленно меняющейся составляющей

Вынуждеппые колебания будут неср[мметрнчными в следуюпшх случаях:

1) при несил[.метричных нелинейных характеристиках системы;

2) при наличии постоянного или .медленно ме[1яющегося внешнего воздействия (в статических системах);

3) при начичии постоянной или медлешюменяющейся скорости изменения внешнего воздействия (в астатических систе.мах).

В общем случае будем полагать, что к нсли[ейной системе приложены два B[ie-п[них воздействия, вследствие чего ее уравнение в.место (21.2) имеет вид

Q (р)л- + R (;;) Е(х,рх) = 5, (р)/, (О + (jp)h (О- (21-24)

причем/[ (t) - .медленно меняющееся внешнее воздействие, а/2 (О - периодическое ВИСН1НСС во.здейс;твие:

/2 (О = i5 sin со г. (21.25)

Медленно .меняющееся воздействие(f) считается мало изменяющимся ;ia период Гц = - , т. е. предполагается, что возможные частоты изменения/j (г) значительно

ниже частоты со .