2. Нормальный закон распределения непрерывных случайных величин (закон Гаусса). Этот закон имеет вид

fV27T

(11.21)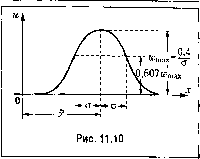

гдест- среднеквадратичное отклонение, а х - .математическое ожидание случайной величины.

График для этого закона изображен на рис. 11.10. Он имеет типичную колоко-лообразную форму.

Анализ условий возникновения нор.малыюго распределения показывает, что оно имеет .место во всех тех случаях, когда случайная величина характеризует собой суммарный эффект большого числа независимых причин. Поэтому нормальное распределение весьма часто встречается на практике.

Для этого закона средпевероятное отклонение будет

д=-о = 0,674о.

За максимальное отклонение, которое может иметь место, обычно принимают

будет больше

величину Дп,ах = Зет, так как вероятность того, что отклонение х-х 3cJ, очень .мала, а именно:

Р(л-.г>3а) =0,003.

Для удобства расчетов составлены таблицы для единичного нормального закона. Для получения этого закона положим х = О и введе.м новую относительную пере-

менную Тогда вероятность того, что текущее значение относительной пере-

менной находится в интервале от -а до +а или сама переменная находится в интервале от -ао до +аа, определится выражением

Ф(а) = -

е с1х =

(11.22)

Для функции Ф (а) составлены подробные таблииы. В качестве иллюстрации приводится краткая табл. 11.2.

Рассмотрим пример пользования таблицей. Пусть имеется некоторая случайная величина х, для которой математическое ожидание х = 10, а среднеквадратичное отклонение составляет о = 4. Определим, какова вероятность того, что случайная величина лежит в интервале 9,5 < х < 10,5. Это означает, что отклонение от математического ожидания должно лежать в интервале -0,5 < Д < 0,5. Для относительных величин это соответствует неравенству

-0,125 < А/о <-НО, 125.

Таблица 11.2. Единичный нормальный закон

Таким образом, а = 0,125. По табл. 11.2 определяем путем интерполяции вероятность Ф (я) =-0,1.

Произведем более сложный расчет. Пусть для той же случайной величины необходн.мо определить вероятность нахождения ее в интервале 11 < х < 12. Так как кривая нормального раснределепия является си.м.метричпой относительно среднего значения случайной величины, то искомая вероятность может быть найдена как половина разности вероятности нахождения случайной величины в интервале -12 <х < 12 и вероятности нахождения в интервале -11 <х< 11, т. е.

Р(11<х<12) = или для отклонений

Р(-12<х<12)-Р(-11<х<11)

Р(11<х<12)=(-<<)-(-<<>.

Перейдя к относительным величина.м, получаем в результате искомую вероятность

Р(11<х<12) = Ф 5>-ФМ5).0.383-0,197 рЗ

Характеристические функции. Введем в рассмотрение функцию g (jX), связанную с плотностью вероятности w (х) взаимным преобразованием Фурье:

Эта функция называется характеристической. Ее основные свойства следующие. Если случайная величина у = ах + Ь,то

gJjX) = ei g,{jX).

(11.24)

rV2J

]кк-

{x-xf 2а

dx = -

rV27i.

dxn =

= ехр

jax--

(11.26)

По характеристической функции .могут быть найдены моменты случайной величины. Разлагая g (JX) яМ[е ] в первой формуле (11.23) в ряд Маклорена, имеем

Я(Д) = 1т:Я<Ч0)Х4р,

M[e] = ±M[x\ + M[R,A.

i--0

(11.27)

(11.28)

Из сравнения (11.27) и (11.28) можно получить формулу для момента т-то порядка:

M[x J=/- g( 40). (11.29)

Аналогичным образом можно получить формулу для центрального момента т-го порядка:

М\(х-£Г] = Г

re--giJX)

(11.30)

J).=0

Формулы (11.29) и (11.30) могут быть использованы для вычисления моментов.

Векторные случайные величины. Пусть имеется совокупность случайных величин X; (г = 1, 2.....п). Такая совокупность может быть представлена в виде матрицы-столбца. Если физические размерности всех величин одинаковы, то матрица-столбец может быть отождествлена с вектором. При разных размерностях переход к век-Тору может быть сделан после нормирования (введения весовых ко.зффициснтов).

Пусть, например, имеются две непрерывных случайные величины х, и х-. Для них может быть введена двумерная плотность вероятности w (х Х2). Если величины Xi и Х2 независимы, то w (х Х2) = (х,) zei. (хг).

Вводится понятие смешанного .мо.меита т-то порядка, где т = q+ s,

щх(Х2\= I х/хХх Х2)Лг,Лг2

(11.31)

Если случайная величина 2 = х + г/, где .т и г/ - независимые величины, то

g.O) = g.v()g;y(;)- (11.25)

Для нор.малыюго закона распределения (11.21) характеристическая функция бу-