Рассматривая характеристическое уравнеиие системы

ТуТУ + {Ту + Т)р -p + K,Tj> + K,- О,

можно убедиться, что в системе возможно получение устойчивости при выполпении условия

Г (Г, + Г,)-(Г, + Г )2

- (9.16)

К,<-

y>.\\

ИЛИ в ином виде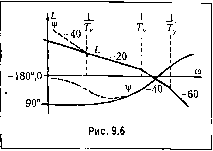

Ту + Т-

(9.17)

Нетрудно видеть, что при Т °° (это будет при отсутствии интегрирующего привода в изодромном механизме) условие устойчивости переходит в неравенство

К< - +-,

у м

(9.18)

которое справедливо для исходной схе.мы, изображенной иа рис. 6.4. При достаточно больших 311ачениях постоянной времени изодро.много .механизма Г , что соответствует .малому передаточному коэффициенту интегрирующего привода к = -, ус-

ловия устойчивости (9.16) и (9.17) будут .мало отличаться от условия устойчивости (9.18) исходной схе.мы. Таким образом, введение изодромпого механи.зма с относительно большой постоянной вре.мени Г дает повьнпение порядка астатиз.ма па единицу ири воз.можности практически сохраги1Ть условия устойчивости в систе.ме, куда этот механизм вводится.

Это обстоятельство можно проиллюстрировать также па логарифмических частотных характеристиках (рис. 9.6). В соответствии с выражением для передаточной функции разомкнутой системы (9.14) можно записать:

i(a)) = 201g

(9.19)

(9.20)

Ч/(со) = (-90° - arctg (оГу - arctg шТ ) - 90 -ь arctg шГ .

Сравнивая эти выражения с формулами (9.6) и (9.7), справедливы.мп для исходной схемы, можно заметить, что ири относительно большо.м значении постоянной времени Г логарифмические характеристики системы с изодромтгым стройство.м

будут и.меть отличие только в низкочастотной области при а)<-. Для частот (х -

Т, и

дополнительный множитель в (9.19) обращается в единицу, а дополнительный фагю-

вый сдвиг в (9.20) равен нулю. Таким образом, при ш>7 логарифмические частот-

ные характеристики системы с изодромпым устройством практически пе отличаются от логарифмических характеристик исходной схемьг В частности, в районе нуля децибел для л. а. X. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одинаковому запасу устойчивости.

На рис. 9.6 сплошны.ми линиями показаны л. а. х. и л. ф. х. для исходной схемы, а пунктирными - изменения, даваемые введением изодромного устройства с относительно больнгой постоянной времени.

Следует заметить, что введение изодромного устройства с большой постоянной вре.мени образует систему, динамические качества которой .могут оказаться сравнительно низкими. Это объясняется тем, что введение такого устройства улучшает вид амплитудной характеристики только в низкочастотной области (рис. 9.6). В результате коэффициенты ошибки, следующие за те.м коэффициенто.м, который обращается в пуль, .могут не только пе уменьшиться, тю даже возрасти.

В рассмотренном выше примере при введегии! изодромного устройства обратился в нуль коэффициент С] (9.15). Однако в следующие коэффициенты в качестве дели-

теля входит добротность но ускорению =--. При большом значении постоян-

ной времени Г добротность системы по ускорению получается малой и коэффициенты ошибок с- Сз,... сильно возрастают.

Для дальнейшего повышения порядка астатизма систе.мы могут п])имсняться не один, а два, три и т. д. изодромных устройства. В этом случае можно получить гювы-шение порядка астатиз.ма на один, два, три и т. д. в зависимости от необходимости. На рис. 9.7 в качестве примера приведена структурная схема системы с тремя изод-ромными устройства.мн. Если исходная система имеет, например, астатизм первого порядка, то система рис. 9.7 с изодромными устройствами будет обладать астатиз-мом четвертого порядка. В этом случае для коэффициентов ошибок будет и.меть место равенство Сд = Cj = = С3 = 0. Как и ранее, при соответствующем выборе постоянных времени изодромш>1х устройств Г , =-, Tj,2 =- и 7 ,з =- можно сохранить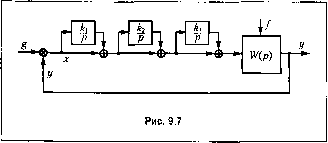

практически те же условия устойчивости, что и в исходной системе.

Управление по производным от ошибки. В боль-пшпстве стучаев управление но производным от ошибки имеет целью повысить запас устойчивости системы, что позволяет увеличить коэф-

Лиффьчюнцируютий элемент

Рис. 9.8

Рис. 9.9

фициент передачи разомкнутой системы и те.м са.мы.м улучиипь точность. Это будет рассмотрено более подробно в главе 10.

Однако управление но производным от ошибки может са.мостоягельно повышать точность системы даже в том случае, когда сохраняется неизменным коэффициент передачи. Физика этого явления заключается в том, что при введении управлепи>; по производным система начинает чувствовать ие только наличие оншбки, но и тенденцию к изменению ее величины. В результате она более быстро реагирует на появление задаюпшх и возмущающих воздействий, что снижает опшбку.

Структурная схема введения производной по ошибке и.зображена па рис. 9.8.11е-редаточная функция части прямого канала в.месте с включенпы.м дифференцирую-пшм элеме15том может быть представлена приближенно (в предположении, что диф-ферепцирующий э.темент является идеальным) в виде

д(р)=1 + 7;р, (9.21;

где Гд - постоянная времени дифференцирующей цепи.

В качестве дифференцируюпщх элементов .могут, например, приме1гяться уст ронства, изображенные на рис, 4.20 и 4.21.

Рассмотрим в качестве примера ту же следящую систему (рис. 6.4). При введениг производной от ошибки при помощи тахогенераторов, установленных на командно! и !1С1!ОЛ!!ителы!ой ОСЯХ, электромеха!!ическая схема будет иметь в!1Д, изображе!ГШ)!1 !ia рис. 9.9. Здесь !!ри!!ять! следую!![ие обоз!!ачения: СКВТ - синус!10-косинусн1)1( вращающиеся трансфор.матор!я, ТГ - тахогенераторы, Д - двигатель, р - ре;дуктор

Передаточная фу!!К!щя разомкнутой системы может быть !!олучена умножени ем (9.1) на !!ерелаточную фу11К!шю (9.21). В резу.Ш)Тате !!Олучим

К(\ + Т,р)

р(1 + Г,я)(1 + Г,р)

(9.22

где !!остоя!П1ая вре.ме!1Н Т, !1редста!У!яет собой от!10!пение передаточпо!-о коэффициент тахоге1!ератора к передаточному коэффицие!!ту чувс,Т!5ителы!01о элеме!!та (СКВТ), т. е.

рад рад