(18.31)

причем линейная часть может иметь структуру любой сложности (и любой порядок уравнения).

Уравнение нелинейного звена

= f(.v px,)

в колебателыгом процессе после гармонической линеаризации запишем в виде

, а(а, (о)

(18.32)

В частности, для нелинейной характеристики= (х,) без гистерезисной петли будет

X2 = <7(a)xi.

Уравнение нелинейного звена (18.32) .записано, как видим, без учета высших гармоник, фигурировавших в предыду111е.м параграфе. Это сделано отнюдь пе потому, что они .малы. В отдельно взятом нелинейном звене при подаче на вход х, = а sin Ш в общем случае па выходе обязательно появятся высшие гармоники. Однако в замкнутой автоматической системе (рис. 18.4, а) линейная часть имеет обычно а.мплитудпо-частот-иую характеристику одного из двух видов, показанных на рис. 18.4, б. По-этому высшие гармоники, имеющиеся у переменной х2, гасятся линейной частью и переме1П1ая x, ока;зывается достаточно близкой к синусоиде: х, = а sin ш. В тако.м виде и буде.м искать приближенное периодическое репге-ние для нелинейной автоматической системы. Свойство линейной части систе.мы, определяющее вид амплитудно-частотной характеристики типа изображенной на рис. 18.4, б, именуется свойством фильтра. Аналитическое обоснование сказашюго см. в книге f72,§ 2.2).

Как видим, в коэф4)ициенты уравнения (18.32) входят амплитуда а и частота ш искомого колебательного процесса.

Нелинейное [ ,

звено

Линейная

часть

§ 18.2. Алгебраические способы определения автоколебаний и устойчивости в нелинейных системах первого класса

Основываясь на вышеизложенной гармонической линеаризации, состави.м гармонически лииеаризоватгое уравнение всей .замкнутой нелинейной авто.матической системы в целом. Пусть известно дифференциальное уравнение линейной части систе.мы

На основании уравнений (18.31) и (18.32) можно наиисать гармонически линеаризованное характеристическое уравнение замкнутой нелинейной системы в виде

Q(P) + R(P)

Ч + -Р

= 0 (18.33)

с теми же особенностями в коэффициентах, что и в уравнении (18.6), онисащщгми в § 18.1.

В том случае, когда в замкнутой системе возникают собственные незатухающие колебания постоянной амплитуды а = а и постояшюй частоты со = со (автоколебания), коэ(})фициепты уравнения (18.32), а значит, и коэф(}1ипиенты характеристического уравнения (18.33) становятся постоянными. Вместе с тем из линейной теории известно, что появление указанных колебаний в системе при постоянных коэффипи-ентах соответствует наличию нары чисто мнимых корней в характеристическом уравнении системы.

Следовате;1Ьпо, можно обнаружить в замкнутой нелинейной систе.чсе появле1Н-1е незатухаюищх собственных колебаний видах = sin со г (а = const, со const), подставив в характеристическое уравнение (18.33) р =7С0 . Если эта [юдстановка р =7С0 соответствует каким-нибудь вещественным положительным значениям а = а и со= со прн заданных пара.метрах системы, то такие колебания возможны. Но подстановка р = jco в характеристическое уравнение с постоя1тыми коэффициентами эквивалентна отысканию границы устойчивости линейной cncTeNUM. Следовательно, иоявлеине неза гухаюипгх собственных колебаний в нелинейной системе можно обнаружить при-.менение.м к характеристическому уравнению (18.33) любого из .методов определения границы устойчивости линейной системы, изложенных в главе 6.

Основной способ определения периодических решений. Используем пепосред-ствешгую подстановку р =усо в 1армопически липеаризоващюе характеристическое уравпение, а именно

Q Oco) + ?0 ) [<?( . )+><7( . )1 = О, (18.34)

при неизвестных постоянных значениях амплитуды а и частоты со, входящих в коэффициенты ди q, причем для однозначной нелинейной xapaKTepHCTHKHf(x,) будет

Q(Jm) + R(j(a) <?( ) = 0.

Выделим в выраже1[ии (18.34) вещественную и .мнимую части:

Х(со)+;Т(со) = 0, (18.35)

и введем для частоты и амплитуды искомого периодического ренюния обозначения: (О = со , а = а . Это дает два уравнения:

Х(со , ) = 0, У(со, а ) = 0,

(18.36)

из которых н определяются неизвестные частота со и амплитуда а .

Если уравнения (18.36) не и.ме1от положите.твиых пеп1ественных решений для а и со , то периодические репюния вообпю (а значит, и автоколебания) в данной нелинейной системе невозможны.

Иссчеловапие устойчивое ги периодического решения лается ниже.

С HO.MOHibK) уравнений (18.36) .можно не только определять частоту со и а.мплиту-ду а автоко.чебаиий ири заданных параметрах системы, но и построить графики зависимостей (0,1 и я от какого-либо пара.метра системы, например коэффициента усиления k. Для этого нужно считать в уравнениях (18.36) параметр к переменным и записывать эти уравнения в виде

Х(а) ,а к) = 0, Y(m, a, k) = 0.

(18.37)

Отойда можрго 1шйти зависимости

а = а (к), со = со ()

и построить их, например, в виде графиков рис. 18.5, а, б. На основании этих графиков можно будет выбирать пара.метр к так, чтобы алиглитуда автоколебаний б1>1ла достаточно малой, чтобы частота их пе была опасной для данной системы или жс, наконец, чтобы автоколебаний пе было вовсе (к < г ).

Кроме того, с но.мощью тех же уравнений (18.36) можно строить линии равных значений а.милитуды и частоты автоколебаний на плоскости двух каких-либо параметров системы, 1шпример к и 7. Для этого уравпепия (18.36) записываются в виде

х(Чр >/лП=о,

Г(со ,а ,;,7-) = 0.

Зададимся ра.зличными числовьпми значениями амплитуды а и получим для каждого из них по уравнениям (18.38) зависимости

к = к(ш ) и Г=7(а) ).

После этого, меняя со , можно построить по точкам соответствуюпите кривые й = con.st в координатах (к, т), как показано сплопнп>1Ми линиями па рис. 18.5, в. На этих кривых получаются отметки частот (О , которые также .можно сюедипить (пунктирные кривые).

График рис. 18.5, в позволяет выбирать значения двух параметров (к и О нелинейной системы. Если такие графики построить для ра.зличпых в(х$можпых структурных схем систе.\гы, то можно будет выбирать также и паивы-годнейшую структурную схему проектируемой замкнутой авто.матической системы с учетом нелинейностей.

Использование графиков коэффициентов гармонической линеаризации. Во многих задачах коэ(}1фициеиты

(18..38)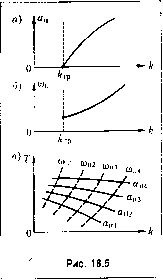