В характеристическом полиноме разомкнутой системы С{р), т. е. в полиноме знаменателя Щр) имеется два вещественных отрицательных корня р--,

1 1 2

Р2 И ОДИН вещественный положительный корень ft =+- Наличие после-

днего свидетельствует о неустойчивости управляемого объекта (ракеты) и разомкнутой системы в целом. Поэтому система автоматического управления создается, в первую очередь, для обеспечения устойчивого полета ракеты.

В данном случае /= 1. Таким образо.м, для устойчивости замкнутой систе.мы а. ф. X. разомкнутой системы должна охватывать точку (-I,/)) на угол л против часовой стрелки.

Для построения а. ф. х. находим модуль и фа.зу (см. табл. 6.1)

Л(©) = 1У(;©) =

X7l + 7fa7

(l + r(,V)7l + r(o

i/((o) = -л + arctg ш7 - arctg соГз.

При изменении частоты от со = О до ш = < модуль изменяется от Л(0) = К до у\(оо) = о, а фаза - от i/(0) = - л до (°°) = -л. Ecjhi Г, > то при Mt О и 1)аз-

ность арктангенсов больше нуля, а. ф. х. расгюлагается в третьем квадранте (рис. 6.15) ипрп/С> 1 охватываетточку ( 1,у0) на угол +л,т. е. против часовой стрелки. Вэто.м случае замкнутая система устойчива. Если 1\ < Т, то а. ф. х. располагается во втором кзадра1гге и при К > 1 охватывает точку ( -1,;0) на угол -л. В этом случае замкнутая система неустойчива. Если же К < 1, то при любых значениях Г, и Т2 а. ф. х, разо.\иснутой системы не охватывает точку (-1,;0) и замкнутая система неуспойчи-ва. Таким образом, замкнутая система устойчива, если 7С> 1, Г, > Г2. Эти условия совпадают с пайденны.ми ранее при помощи критерия Гурвица.

В ряде случаев более удобной может оказаться другая (})ормулировка критерия Найквиста. Она основана на том, что величина и знак угла охвата точки ( l.jO) зависят только от того, как и сколько раз а. ф. х. разомкнутой системы пересекает отрезок вещественной оси, расположенной левееточки (-1,70), и ие зависят от ее прохождения правее этой точки. Например, нетрудно убедиться, что все три а. cj). х., изображенные на рис. 6.16, охватывают точку (--1,70) на угол -ьл.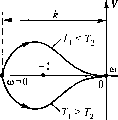

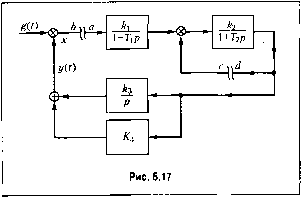Щр) =

\ + ТуР i + k + Tp

p(\ + T,p){\ + k2+T2p)

Разомкнем теперь ту же систему не па входе первого звена, а в цепи обратной связи второго звена (точка с соответствует входу, а точка d - выходу). Передаточная функция разо.мкнутой системы в этом случае

W\p) = -

\ + Т2Р

k2p(\ + T,p)

\ + Тр \ + Т2Р

- + h

р(\ + Тр){\ + Т2Р) + AlAjAa + kk2kip

Выделим на венюственной оси критический отрезок (рис. 6.16). Тогда для устойчивости замкнутой системы необходимо и достаточно, чтобы сумма переходов амплитудно-фазовой характеристики замкнутой систе.мы через критический отрезок

при из.менении частоты от О до была равна , где / - число корней с положительной вен[ествеи-ной частью в характеристическом полиноме разомкнутой системы. При этом переход сверху вниз считается положительным (+1), а снизу вверх - отрицательным (-1).

Если при (о = О а. ф. х. начинается па критическом отрезке, то имеет место - перехода с соответствующим знаком. Например, иа рис. 6.15 (/ = 1) при /С > 1 а, ф. х. совершает перехода, если Г, > Г2 (замкнутая система устойчива) и перехода, если

Ту < Т2 (замкнутая система неустойчива). При К < 1 переходов нет п замкнутая система неустойчива. На рис. 6.12 (/ = 0) имеется -1 переход на частоте Q, и +1 па частоте Сум.ма переходов равна нулю и за.мкнутая система устойчива.

Сделаем теперь замечаште, касающееся использования для определения устойчивости замкнутой системы передаточной функции разо.мкнутой системы.

В случае многокоитурной системы управления раз.мыканиеее для получения передаточной функции разо.мкнутой систе.мы можно делать, вообще говоря, в произвольно.м месте. Рассмотрим, например, систему, структурная схе.ма которой изображена на рис. 6.17.

Разомкнем систему на входе первого звена. Тогда, рассматривая точку а как вход, а точку /; как выход, получаем передаточную функцию разо.мкнутой системы

Передаточные функции W(p) и W(p) получились различными. Однако им соответствует одно и то же характеристическое уравнение замкнутой систе.мы 1 + W(p) = 1 + WXp) = О, которое имеет вид

rj.j) + (Г, + Т2 + k2T,)p + (1 + 2 + fAk.yp + kkk = 0.

По.зтому для определения устойчивости можно пользоваться передаточной функцией разомкнутой системы, полученной раз.мыканием исходной системы в произвольной точке, в которой выполняется условие детектирования.

Однако передаточные функции W(p) и W(p) имеют различие. Только передаточная функция W(j)) связывает между собой изображения управляемой величины и оншбки, и только она связана с передаточной функцией замкнутой системы Ф(р) известны.м соотношением

wip)=mi.(pL,

Х(р) 1-Ф(р)

Передаточную функцию при размыкании па входе первого звена в дальнейшем будем считать главной передаточной функцией разо.мкнутой системы и именно ее иметь в виду ири рассмотрении методов определения качества управления и синтеза систем управления.

§ 6.5. Определение устойчивости

по логарифмическим частотным характеристикам

Для определе}1ия устойчивости по критерию Найквиста можно строить не амплитудно-фазовую характеристику, а логарифмическую амплитудную частотную характеристику (л. а. x.) и логарифмическую фазовую частотную характеристику (л. ф. x.) разо.мк}1утой системы.

Построение л. а. х. производится по выражению

Д со) = 20 Ig А((й) = 20 \g\W{j(ii)

где Л(а)) - модуль частотной передаточной функции разомкнутой системы (6.23).

Построение л. ф. х. производится по значению i/(a)) частотной передаточной (})ун-кции (6,23). Для построения л. а. х. и л. ф. х. удобно использовать стандартную сетку изображенную па рис. 4.19.

Наиболее простое построение получается, если передаточную функцию разомкнутой системы .можно свести к виду