После сделанных предварительных заключений перейдем к определению амплитуды и частоты автоколебаний в тех случаях, когда последние имеют место.

В случае идеальной релейной характеристики в соответствии с (18.211) и (18.18) имеем

-M (a) = --L = -a (0<а<оо) (18.222)

W (a) Ас

(М (а) заполняет всю отрицательную всществепную ось, рис. 18.44, а). По.этому IV (/со) при отсутствии жесткой обратной связи (сплошная кривая) пересекает ее, а при наличии жесткой обратной связи Eie пересекает (пунктирная кривая). В первом случае получаем точку пересечения D, определяющую периодическое решение (а , со ). Оно будет устойчиво (т. е. соответствует автоколебаниям), так как кривая W (/со) охватывает участок прямой -М (а) с меньшими амплитудами (линейная часть согласно (18,221) пейтралыш, вследствие ч.его этот критерий можно примеЕ1ять). Во втором же случае кривая Wj, (joi) пересекается с пря.мой -М, (а) только в точке, где а 0,0i = т, е. автоколебания отсутствуют (конечная амплитуда получится, если учесть постоянную Гз)-

Амплитуда а автоколебаний в перво.м случае определяется по расстоянию / (рис. 18.44, а) налипни -М (а) до точки пересечения, причем с учетом (18.222) нолучае.м

п= (18.223)

где /берется из грас)ика или вычисляется по формуле

приче.м величина частоты автоколебаний со находится из условия

если Ujj (со ) и V, (со ) обозначают вещественную и мнимую части выражения (/со) при Р = 0, т. е.

W.О) = У. (18.224)

(Г,;со+1)(Г;со+1);со

Отсюда видно, например, что с увеличением 23 увеличивается а\гплитуда автоколебаний.

Для характеристики реле в виде рис. 18.20, а поведение системы без жесткой обратной связи поясняется рис. 18.44,6. Здесь автоколебания .Moiyrотсутствовать (кривая / рис. 18.44, б), В03.М0Ж1К) одно периодическое решение (кривые 2 и 3, пересекаю-пшеся в точке В) или два периодических решения (кривые 2 и 4, пересекающиеся в точках А и С). При .этом кривая 3 соответствует мепыии.м, а кривая 4 - большим значениям т в релейной хараЕстеристике (см. рис. 18.39). Точки ВиА отвечают устой-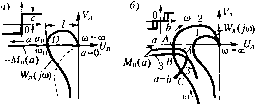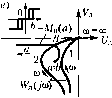

-W (fl)

Рис. 18.44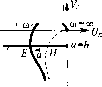

чивым автоколебаниям. Точка С отвечает неустойчиво.му периодическому процессу, что .может о.зпачать устойчивость системы в мало.м (при а < a(j) и стремление к автоколебательному ггроцессу с а.мплитудой а = Яд в больпюм. Величины амплитуды и частоты автоколебаЕ1ИЙ определяются по са.мим кривы.м в точка.х их пересечения.

В данном случае влияние величины 23 без жесткой обратной связи заключается в том, что с увеличением 23 осупюствляется переход от кривой 1 к кривой 2 (рис. 18.44, б), т. е. автоколеба1ШЯ в системе появляются только тогда, когда 23 Ф взойдет некоторое граничное значение, определяемое мо.мептом касания кривой 1 с кривой 3 ила 4.

Апачогичио определяются автоколебания и при наличии жесткой обратной связи, как показано на рис. 18.44, в.

Наконец, нри чисто гистерезисной характеристике реле иолучае.м то.аько автоколебательный процесс (рис. 18.44, г), амЕ1литуда и частота которого без жесткой обратной связи определяются точкой Е, а при наличии жесткой обратной связи - точкой Я.

Во всех рассмотренных случаях, как и вообще в рассматриваемом частотном методе, чере.з а обозначается а.мплитуда автоколебаний входной величины пелпнейного звена, т. е. в дапЕЮМ случае величины х. Чтобы определить а.мп.читуду о автоколебаний уЕфавляе.мой величины 8 (температурЕ)е), надо еайти передаточную функцию, связывающую величины X и 8:

и, следовательно,

0 =

Для системы без обратной связи ( . = 0)

Ана;к)гично можно определить амплитуду первой гармоники автоколебаний для других переменных в данной системе.

ных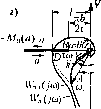

Рис. 18.45

Учет временного запаздывания в реле. В рассмат рпваемо.м выше ирн.мере системы стабилизации те.мпературы считалось, что в характеристике реле рис. 18.20 величины А 6.2, b заданы постояттыми, т. е. считалось, что характеристики реле имеют обычный гистерезисный вид с задашгым по входной координате отставанием в срабатывании реле. Теперь же буде.м считать, что и.меются данные запаздывания во времени срабатывания и отпускания реле (одинаковые). Такое нел1П1ейное звено с запаздыванием .можно разбить на два .элемента: 1) обычное нелинейное звено, характеризующееся графиком рис. 18.45, били в, и 2) .элементзапаздывания (рис. 18.45, а), 01Н1сывае-мый уравнением

Тогда можно будет записать выражение а.мплитудно-фазовой характеристики линейной части системы вместе с элементо.м запаздывания в виде

JXM

(18.225)

Правило построения такой характеристики описано в главе 6.

Пусть реле (после выделетш элемента запаздывания) характеризуется гра(()Ико\[ рис. 18.45, б. В это.м случае для системы с жесткой обратной связью получим соответственно кривые W;., (/со) и W (/со), и.зображенныс на рис. 18.45, г, а также прямую -М (а) tra основании фор.мулы (18.213) п рис. 18.40, а. Если кривые W.,. (/со) и -М (а) пересекаются, то будут иметь место автоколебания. По, как видно из рис. 18.45, г, при достаточно ма;1ых запа.здывапияхх указанные кривые могут не пересекаться, т. е. автоколебаний не будет.

Здесь, как и в линейных системах, .можно опредс>лить к[)Итическое время загнгзды-вания, до которого автоколебания отсутствуют, без построения кривой W., (/(О) только по кривым W (jw) и -М (а). В самом деле, в критическом случае некоторая точка