или после объединения некоторых уравнений

(Г,р + 1) = Л-

(6.86)

Исключив отсюда переменные и т], приходим к одному дифференциальному уравнению данной систе.мы авто.матнческого управления:

(7iV+?2/ + l)(7;P + l) которое преобразуется к виду

(1 + Ье-) + -(!- Ье- ) +Ш + be ) \Ф = О, Y J

(Т,р+Т2Р + ШР + ) +

(т;р+т,р+\){т,р+1)+

Y + l Y-l

(6.87)

е-Р\ф = 0.

Это уравнение имеет в основно.м тот же вид, что и уравнение системы с запаздыванием (напри.мер, (6.40)). Здесь оно определяет величину Ф, через которую затем находятся из вьппепаписаппых соотношений управляемая величина ф; и другие. Параметр т в этом уравнении согласно (6.82) и (6.,58) вычисляется по формуле

х = 2. а

(6.88)

т. е. т есть удвоенное вре.мя прохождения звука в газе по данному трубопроводу.

§ 6.8. Устойчивость двумерных систем с антисимметричными связями

В практике встречаются двумерные системы управления с аптисимметричпы.ми связями. Структурная схема такой системы изображена на рис. 6.29. Она содержит два идентичных канала с одинаковыми передаточными функциями W(,(j>) = W(p) V2(/) и антисн.мметричные связи. К такому виду сводятся некоторые гироскопические устройства, двухканальные системы слежения и др.

Матрица-столбец выходных (управляемых) величии связана с матрицеГ1-столб-цом ошибок выражением

= W{p)x.

(6.89)

Характеристическое уравнение замкнутой системы:

\E + W{p)\=

= (l + lУo) + Ж?=0.

(6.90)

Здесь E - единичная матрица 2x2.

Для расчета устойчивости введем в рассмотрение ко.милсксные величины

х = Х( + 7x2.

(6.91)

(6.92)

Матричная зависимость (6.89) дает два равенства:

y,=W{p)x,+aWQ{p)x2, z/2=-aWo(p)Xi+Wo(p)X2.

Умножая второе равенство нау и складывая, нолучае.м для ко.мплексиых величин

y*{\-}aW,{p)x=W,{p)x\ (6.93)

Здесь введена эквивалентная передаточная функция разо.мкнутой двумерной системы

Для .дальнейшего расчета может использоваться критерий Найквиста в своей обычной формулировке. Однако для построения а. ф. х. разомкнутой системы следует использовать частотную передаточную функцию

W.Ow) = (l-7 )WoOw).

Ее модуль

(6,94)

а фаза

w,( i=Mo(; )l->/i.

Жэ(м) = \/о(со) - arctg а.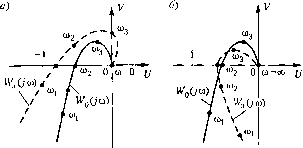

Рис. 6.30

По сравнению с исходной а, ф. x. Wq(jw) модуль

увеличивается в

раз и

появляется дополнительный фазовый сдвиг а = -arctg а. Это означает, что каждая точка исходной а. ф. x. удаляется от начала координат и но-ворачивается но часовой стрелке, если а > О (рис. 6.30, а), и против часовой стрелки,

если а < О (рис. 6.30, б). Заметим, что в случае перехода к комплексным вепгчинам у* и х* .можно произвести расчет по а. ф. х. исходной однокапальпой системы W()(;co). В этом случае колебательная граница устойчивости будет при выполнении условия

W,(jb)-(l-ja)WQ(jo)--{. (6.95)

Рассмотренный метод позволяет упростить определенные устойчивости двумерной системы по сравнению с использованне.м результирующего характеристического уравне[П1я (6.90), так как требуют рассмотрения передаточной функции Wip) одного изолированного канала.

Глава 7

ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

§7.1. Общие соображения

Дифференциальное уравнение обыкновенной линейной системы автоматического управления, записанное для ошибки управления, согласно (5.6) и.меет вид

D{p)x{t) = Q(jj)g(t) + N(p)f(tl

(7.1)

где р-~ - алгебраический оператор дифференцирования; g{L) - задаюп1ее

воздействие;/(г) - возму1цаюц1ее во.здействие.

Решение линейного дифференциального уравие1И1я с постоянными коэффици-ента.ми (7.1) будет

х(0=х (0+л- (0. (7.2)