Таблица 12.1. Стандартные передаточные функции разомкнутой системы с астатизмом первого порядка при п г 2 4

Если нужно выбрать два или несколько параметров системы, то такого рода вычисления нужно проделать несколько раз, меняя каждый раз один из параметров при заданных значениях всех остальных.

Вычисление корней при это.м можно производить нрн помощи стандартных программ для цифровых маннш с выводом траектории корней на экран дисплея. Другой способ построения траекторий корней рассмотрен в [91].

§ 12.4. Метод стандартных переходных характеристик

Для получения необходимых значений коэффициентов нередаточной функции разомкнутой системы можно воспользоваться стандартными переходными характеристиками. Для большей общности .эти характеристики строятся в нормированном виде, В этом случае ио оси времени откладывается относительное время т = QqZ, где Qq - среднегеометрический корень характеристического уравнения, определяю1Ций быстродействие системы.

При построении стандарттилх переходных характерргстик необходимо задаться определенным распределением корней характеристического уравнения.

Ниже приводятся стандартные характеристики и соответствующие передаточ-!пле функции [44].

Для систем с астатизмо.м первого порядка корни ири]шты веп1ественпыми, причем они составляют арифметическую прогрессию. В табл. 12.1 приведены передаточные функции разомкнутой системы для различных порядков характеристического уравнения п = 2 -ь 4, получающиеся при этом значения перерегулирования а% и добротности по скорости /С,.

Нор.мироваиные переходные характеристики для каждого случая приведены иа, рис. 12.1, а.

Для систем с астатизмо.м второго порядка корпи также приняты вен1ественными, приче.м они составляют геометрическую прогрессию. Соответствующие передаточные функции приведены в табл. 12.2, а переходные характеристики - па рис. 12.1, б.

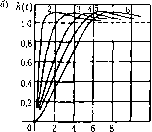10 По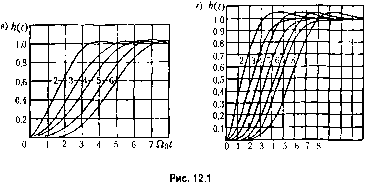

9 10 WClt

Таблица 12.2. Стандартные передаточные функции разомкнутой системы с астатизмом второго порядка при п = 2 + 6

Использование метода стандартных переходных характеристик для синтеза зак-лк:)чается в том, что для принятой структурной схемы выбирается приемлемый вид переходного процесса. Это позволяет установить необходимое значение среднегеометрического корпя Qg. Далее оказываются известными все ко.эффициепты желаемой передаточной функции системы. Введением различных корректирующих средств необходимо добиться того, чтобы коэффнциент1>1 реальной передаточной функции были возможно ближе к коэффициентам желаемой передаточной функции.

Этот метод может применяться и в то.м случае, когда важно обеспечить требуемую точность работы системы, которая может быть задана, например, при 1юмо1ци коэффициентов ошибок. Тогда ири заданных значениях коэффициентов ошибок .можно определить требуемое значение К, или К, а по ни.м найти величину Qq. Далее расчет ведется так, как описано выше.

Недостатком рассмотренного метода является го, что при построении станда])т-пых переходных процессов приняты веществешияе корпи. Это во многих случаях не приводит к оггтпмальному решению. Однако стандартные переходные характе])ис-тики можно сравните.тьно просто построить для любого другого расположе1итя корней, в том числе п для комплексных корней. Предлагается, например, такое решение [44]. Пусть характеристическое уравнение затгсано в виде

р + ДоР + Л21р +... + о=0,

где Q.q - среднегеометрический корень.

Если принять все корни рав1И)1.ми и веществениы.ми, то это характеристическое уравнение приобретает вид

(p + Q,) = 0. (12.,30)

В этом случае безразмерные коэффициенты Л],..., Л ,.1 являются коэффициентами бицо.ма Ньютона.

Однако переходный процесс затухает быстрее, если характеристическое уравнение при четном п имеет вид

(p42CQoP + q2)f =0 (12.31)

и при нечетном п

(p + Qo)(p42CfioP + o) =0, (12.32)

причем безразмерный параметр затухания С = 0,7 - 0,8.

В таб.!!. 12.3 для случая = 0,7,5 приведены значения безразмерных коэффициентов Л j, ..., Л . J, причем Лц = 1 и Л =--1, для степени характеристического уравнения от 2 до 6.

На рис. 12.1, в приведены нор.мированпые переходные характеристики, соответ-ствую1Т1ие характеристическому уравнению (12.32), если в пего ввести правую часП) ввилей/(г).