w(t-&,&)= lim ДЙ-0

Правая часть этого выражения представляет собой производную от переходной функции по аргументу в, взятую с обратным знаком. Таким образом, для функции веса получаем (рис. 13.1, б)

(13.3)

Как следует из (13.3), функция веса является функцией двух rrepCMeinibix: времени в, соответствующего моменту поступления на вход системы единичного импульса, и текунюго времени t (или т = - в). В связи с этим функцию веса можно изобразить в виде некоторой поверхности (рис. 13.2). Эта поверхность переходит в плоскость tO при t<. Границе перехода поверхности в плоскость соответствует биссектриса f = в. Это обстоятельство объясняется тем, что в реальных систе.мах реакция пе может появиться ранее приложения иа входе системы импульса. По:этому при t<-& функция веса должна быть тождествешго равна нулю.

Сечение поверхности весовой функции вертикальной плоскостью, параллельной оси t (рис. 13.2, б), дает весовую фуггкцию для фиксироващюго момента приложения единичного импульса на входе системы (в = const). Эта функция называется нормальной весовой функцией системы с переменны.ми параметрами:

w{t-b,b), в = const. (13.4)

Она является ггараметрической функцией, так как в нее входит фиксированный параметр Ь = const.

Нормальная весовая функция может быть сделана завнсящей от аргумента T = t-b подстановкой = в + т. В результате получаем функцию

ю(т, в), в = const. (13.5)

w)(i-9,9)

9t,on.st

ffi<t-9,9) .v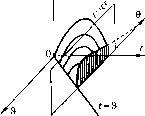

то процесс иа выходе, т. е. функцию веса, в силу принципа суперпозиции можно представить в виде разности двух смещенных па переходных функций с измененным в 1 раз масштабом:

Сечение поверхности весовой фуп-киии вертикальной илоскостью, парал-лельноГ! оси дает кривую, образованную ординатами семейства нормальных весовых функций для фиксированного значения вре.мени t = const (рис. 13.2,6). Эта кривая .может быть получена путем обработки семейства нормальных весовых функций, ностроснных для 1)азлич-иых моментов приложения единичного входного импульса д (рис. 13.3). Получающуюся зависимость будем называть сопряженной функ1[ией веса:

a<t~9,9)

f =const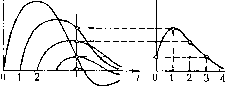

<t-9,9)

3 A t-const

Рис. 13.3

да (t - d, d), t= con.4t.

(13.6)

Она также является параметрической ()упкцией, так как содержит 11арамег[) t = const.

Сопряженная функция веса является функгшей смещения i&, но может быть представлена также как функция apiyMcnra в = t - Ь (рис. 13.2, б), называемого реверс-смещепие.м, поскольку О отсчитывается от точки = г: в сторону, противоположную смещению д. Это осуществляется подстаиовкой в сопряженную весовую функцию :щачения £ - 9 при г = const. В результате получаем

w{e,t-e), f = const. (13.7)

Проиллюстрируем все сказанное примером. Пусть функция веса системы с пе-ре.мснны.ми параметрами имеет вид

Зафшссировав смешение и положив, например, & = -Bq = const, получаем нормальную функцию веса:

ж(-до,до) = е -

или в другом виде при переходе к аргу.менту х = t -

гс;(х,#о) = -

Зафиксировав текущее вре.мя и положив, например, t = tQ = const, получаем сопряженную функцию веса

r (гo-в,г)=e

x{t)= \w{Q)f{t-0)dQ= \w(x)f{t-x)dx.

Перейдя к реверс-смещению вв = t - Ь, имеем

-ао -о

Заметим, что в системах с постоянными параметрами весовая функция является функцией только времени т = - в и пе зависит от момента приложения в входного импульса. Рельеф функции веса (рис. 13.2) в этом случае получается цилиндрическим, а оба рассмотрегшых выще сечения (рис. 13.2, а и б) совпадают по форме и отличаются только знаками аргументов. При переходе к реверс-смещению получаем полное совпадение двух функций веса - нормальной и сопряженной: да (т) = да (G).

Пусть на систе.му (13.1) с функцией веса w (t - Ь, в) действует входной сигнал / (t). Элементарная реакция на выходе системы в произвольный момент времени t>-d будет

(О = w(t- в, в)/ (в) d. (13.8)

Полный сигнал на выходе линейной системы определяется как сунерпозигши элементарных реакций интегрированием (13.8) в пределах от О до t.

x{t)=\w{t-b,b)f{b)db. (13.9)

Так как при Ь> t функция веса равна нулю, то выражение (13.9) можно также записать в виде

x(t) = \0(t-m)f(b)d-b. (13.10)

Из двух последних выражений видно, что в ннтеграчьиом уравнении связи между входной и выходной величина.ми используется сопряженная функция веса (13.6), т. е. разрез рельефа функции веса (рис. 13.2, б) вдоль аргумента Ь.

Если использовать реверс-смещение 6 = - б, то интегральная связь (13.9) .может быть представлена в виде интеграла свертки

x{l)=\w{B,t-)f{t-Qi)dO. (13.11)

Как уже отмечалось, в случае постоянства параметров систе.мы функция веса зависит только от вре.мени {t - Ь). В .этом случае формула (13.11) переходит в интеграл свертки (7.44)