При построении л. а. х. для систем с ЦВМ можно пе вводить снециачьного обозначения для нсевдочастоты X, а употреб-Цять обычное обозначетте со, считая, что в области рабочих частот (левее частоты среза) это есть частота входного воздействия, а в высокочастотной области она переходит в нсев-дочастоту.

Сделаем теперь два замечания. Первое относится к сл\11аю на.!1ичмя в передаточной функнии непрерывной части (1,5.,33) сомножителей, соответствующих колебатсльпы.м звеньям с и.ередаточной функцией

Рис. 15,8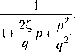

Если выполняется условие (Г< 2, то дискретная частотная передаточная (})ункция для подобного сомножителя совпадает с частотной передаточной функцией непрерыв-иого звена и она может быть гюлучепа подстановкой=jX и умножением на (1 --jXT/2). При qT> 2 построение л. а. х. несколько усложняется вследствие явления трансиони-ровация частот. Однако и здесь не возникает тп<аких принципиальпыхтрудиостей [9].

Второе за.мечание касается последней части условия 2, которое было сфор.мул1гро-вано вьнпе при построе1Н1и л. а. х. для нередаточной футщии (15.33). Если для всех постоянных времени Tj.,;... Г условие 7,< 0,57пе выполняется, то иостроетю л. а. х. делается следующим образо.м. Ст)оится .i. а. х., соответствующая передаточной фут<-ции иенрерывной части (рис. 15.8). Затем проводится вертикальная лття, ссютвет-с1 вующая г)аничиой частоте со, =2/Т.Л. а. х., расположенная левее граничной частот1>1, соответствует низкочастотной части, и она может быть принята в качестве л. а. х. дискретной системы, так как в этой области абсолютная псевдочастота совпадает с обычной частотой: л = со.

Датсе находится формула, соответствующая высок()часгот1Г01 1 части л. а. х. иенрерывной системы, аналогичная формуле (15.41). Пусть, напри.мер, пересечение граничной частоты происходит при наклоне асимптоты -40 дБ/дек так, как это пока;)апо иа рис. 15.8. Тогда уравиепие высокочастотной части будет

W ( ) = -

рЧ1 + Т,Р)...( + Т р)

(к5..э2)

где в = у/к - частота пересечения оси частот асимптотой, имеющей отрицательный наклон 40 дБ/дек.

Раскладывая выражение (15.52) на простые дроби, переходя к W {z), а затем к Wg(jX), получи.м аналогично фор.муле (15.44) для высокочастотной части

\ + JA

(jxy 1+д

(15.53)

Т=Т,+Т2 + ... + Т ,

rj = т;+...+Tif + т;г2+T{r+...+Tj + т,т,+.

Если выполняется условие Т -Т, то формула (15.53) упрощается:

1-дЛ(1-ДГ,) . £ /

(1.5.54)

В соответствии с выражением для И (/Х)строится высокочастотная часть л. а. х., которая показана на рис. 15.8 пунктиром.

Построение фазовой характеристики делается аналогично изложенному вьппе.

Таки.м же способом строится высокочастотная часть л. а. х. при пересечении граничной частоты асимптотой -60 дБ/дек, -80 дБ/дек и т. д. Во всех случаях формирование высокочастотной части делается по сум.ме .Majn>ix постоянных вре.мени, которым соответствуют сонрягаюпше частоты, находящиеся правее фаничпой частоты av 2/Г.

II р и м е р. Произведем расчет следящей системы с астатиз.мо.м второго порядка при слелую1цих исходных данных:

1) .максима.,тЫ1ая входная скорость £2,.,= 10 град/с;

2) макси.мальное входное ускорение е , = 5 град/с;

3) .макси.ма1ьная допустимая ошибка 9п,х 2 угл. .мин.;

4) непрерывная часть содержит постоянные времени Г, = 0,01 с, Т = 0,002 си Гз = = 0,001 с;

5) допустимый показатель колебательности М= 1,5 и М= 1,2.

Требуется определить параметры непрерывной части системы и допустимый период дискретгюсти Т.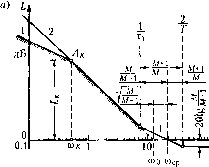

-1/с

Рис. 15.9

0,10 0,20 с

Реши.м задачу виачате для случая Г; 7 , = Уз = О и М = 1,5. Передаточная функ1Н1я HeiipepbiBiroH части разомкнутой систе.мы, структурно устойчивой в замкнутом состоянии, должна иметь вид

Щ(Р)=

гдет, - постоянная времени, вносимая корректируюти.мзвеггомдифференцируюпю-готина.

Так как высокочастотная часть после частоты среза в рассматршзаемо.м идеализированном случае [гредставляет собой прямую с наклоно.м -20 дБ/дек, то вся частотная передаточная функция системы с ЦВМ можеп быть получсиа подстановкой р =]Ь\ где 0) - псевдочастота, и введением дополнительного .множителя (1 ~j<X)T/2):

( Т) /C(l + 7C0Ti) 1-7(0---

о( =--Л-

(jay)

Л. а. X. для нее построена на рис15.9, а.

На этом же рисунке построена запретная зона для л. а. х. на основании условий по точности и в соответствии с рис. 12.8. Базовая частота (12.63)

Ок =

£п-Р:бо=12,2с-.

9,п.х V 2

Требуемое значепие общего коэффициента пе1)едачи разомкнутой системы при совпадении первой аси.мптоты л. а. х. с границей запретной зоны (рис. 12.21)

X = (og=co,=150c-2.