Данные расчета характеристического сопротивлення

Характеристическое сопротивление, умноженное на безразмерный коэфф ициент а/в, ajв Zpy, ом

2t/a

0,200

0,250

0,300

0,350

0.400

0.500

0,600

0,700

1504 762,0 675,3 660,0 608 ,8

68; ,8

710,9 734.9 7Г)8,4 780,4 800,8 819,4 836,4

851.9

866,2

879,3

872.1

634.0

589,0

583,9

593,5

609,0

626.5

644.1

660,9

676.4

690,7

703,6

715,5

726.3

736,2

745,4

684,0 554,0 525,9 524,1 532.3 544,4 557,7 570,9 583,4 595,0 605.6 615,3 624.1

632,2

639.6

646,4

583.7 497.1 476,8 475,7 482,1 491,4 501,7 511,9 521,6 530,6 538,8 546,3 553.2

559,6

0,900

Таблица П.9

Данные расчета характеристического сопротивления

Характерпстнческоесспротивленис, > множеннсе на. безразыегный коэффициент а/Ь, Zpy, ом

2tja

0,025 0,050 0,075

0,100

0,125

0.15)

0.200

0,250

0,300

0,350

0,400

0,500

0,600

0,700

482.2 410.5 403.7 4П.7 423.9 436.4 448.1 458.5 467.8 476,0 483,3 489.9 495,8

0,900

О CJ

ЕГ S H

о s o

C6 H

о 3 s s

о се

я о.

Е >.

к в:

а> 1=;

&

о о ео

о in

оо (N Ю -

о о о

СО Ю СО

00 00 00 (N - -

О (N 00

СО О О О О (N <N (N (N (N

СО О f--

(N 00 СЧ О СО (N СО СО (N (N СЧ (N

CS-ООССлЛО Cb-COh-OOOOOiO CO(NC4(N(N(N(NCO

COCNCCOCOCOCOCOCO

о - 00 Ю <N 00 (N t--

Icoccotottoooo cocococococococococo

00 - lOCO<NlOOO<N-T- (NOO

<N --o *- c4 Ю l-lin CO p О -.OOtDOOO-<NcOTflOOth* OCOCOCOCO***********

(£)а:>-ю01Лооооа1Юосс1Л

о lo 1Л 00 о 00 00 о - ;5Г g

гь-союооюоос . .Я. *-..

So--SSo<NTfcrOOOOCcO;*irtLrt

rrTcjhcooc taiOt--coco -т-со

- KSClOCSrrOOOOCCOlOr-OOLoSSuOUOOt-I-b-t-OOOOGOOOOOOO

r (Cin rrocNCNoo ooo;;£c5b-tDCO

COOCOOCt-OOOCOifeS - -

otD5(SttoooOQOtjiaiaioai

COO <N - f-f-,co Й S S S ot--tt--oooooo

01COtC4(NOtOOtDOO(:DOOt;-C2

о CO о о о to 00 со 00 00 00 о

(N CS CO CO 1Л

С>)тР0000001ЛООСОО

1Л*с01Л1:1ЛЗ;сОсос - о

-X СЧ со 1Л 1Л о Ь- с 00 <

Характеристическое сопротивление при больших заполнениях и больших а/Х мало зависит от частоты из-за эффекта концентрации толя диэлектрической пла-стиной.

4. Предельная мощность, передаваемая по волноводу

В предыдущем параграфе получены все выражения, необходимые для определения предельной мопхности те-редаваемой по частично заполненному волноводу. Пред-, положим, что самым слабым с точки зрения электрической прочности при распространении основной волны будет место максимальной напряженности составляющей электрического поля в воздушной части частично заполненого волновода, т. е. вблизи границы раздела воздух - диэлектрик {х=а/2-t). Такое предположение хорошо согласуется с экспериментальными данными при малых и умеренных заполнениях, что на практике наиболее употребительно, и несправедливо при заполнениях, близких к полному. При этом предположении из выражений (II.6) и (II.7) получаем для предельной передаваемой мощности

аЬ т

иред

макс

cos2 Ы

(II.9)

где £макс - предельная напряженность поля, которая для воздуха-при нормальном атмосферном давлении, нормальной ионизации и нормальной температуре в сантиметровом и дециметровом диапазонах волн составляет 29 кв/см.

Из выражения (II.9) запишем удобное для дальнейшего рассмотрения отношение Рпред к произведению квадрата напряженности электрического поля на поперечное сечение волновода

0,663

макс

Назовем это отношение предельной пропускной способностью волновода. Величины, входящие в формулу (П.10), измеряются Б следуюидих единицах: а, о, к - 3 см, Ey.ui, - KdjcM. Формула (11.10) при отсутствии ди-

электрического заполнения {2 а = 0) переходит в известное из [4] соотношение /пред/(лд(.) = 0.663/п.

Заметим, что при полном заполнении формула (11.10) теряет смысл, поскольку граница диэлектрик - воздух в волноводе отсутствует.

В табл. II.II-11.15 приведены данные расчета пропускной способности по формуле (II. 10) для материалов с диэлектрическими проницаемостями ei = 2, 4, 9, 16 и 25. Для всех диэлектрических материалов при малых толщинах заполняющих волновод пластин и больших значениях а/Я пропускная способность частично заполненного волновода ниже пропускной способности незаполненного. При дальнейшем увеличении толщины заполняющих волновод пластин наблюдается быстрый рост пропускной способности. Такая зависимость пропускной способности, или, что то же самое, электрической прочности, от толщины диэлектрической пластины объясняется тем, что при малых заполнениях часть энергии концентрируется диэлектрической пластиной, но толщина ее недостаточна для того, чтобы область больших значений составляющей напряженности электрического поля оказалась внутри диэлектрической пластины. При дальнейшем увеличении толщины диэлектрической пластины область больших значений составляющей напряженности электрического поля окажется внутри пластины, и с этого момента электрическая прочность частично заполненного волновода будет возрастать. При этом напряженность электрического поля на границе воздух - диэлектрик будет уменьшаться, и в результате пропускная способность частично заполненного волновода будет возрастать. Особенно заметное возрастание пропускной способности волновода наблюдается при заполнениях, соответствующих 2 а0,7.

Приведенное рассмотрение справедливо при условии, что электрическая прочность диэлектрического материала выше электрической прочности воздуха. Практически в сантиметрЪвом и дециметровом диапазонах это Л1ра-веДливо (см. табл. 1.1-1.6) для подавляющего большинства применяемых диэлектрических материалов. Если электрическая прочность диэлектрического материала окажется меньше электрической прочности воздуха, то величина пробивного напряжения для воздуха E/cost должна быть заменена соответствующей величиной про-

rz X X rz

о а.

со X Л

а. С

о со

о о о

ОСТ)СОСОЮСОСТ)СОЮСЧООСО

СО СО СО сч СА Oi Oi со со

ю с£) со со со со со со со

o(3ico,tDTfaiCM(j)COt

CMOOOCMQCOCOCSOltCOOt OlCOtOCTfCOtOl-<COTf

СЧСМСОСОт1*т1**ЮЮ1Л

СОЮООООСО(МСООСОЮОГЮ OOCOOOOOOCOCOOlOOlTtlOt (001СМСОЮСОГ01а СЦСО

сч(мсчечсчсчсосососо

ЮЮ-ЮЮСОЮГЮ-tOCMOO tOC0TflOC0t0001OO(N

CN CN CS CM

tOlOOCMtlOCOlfiCOCO-Tft OCCi-OltOCMtCMCO-<iooi tCOOO-CMCMCOCOTf*

OOOTfTftCOOOllOCOOOlCO (OOllOlOCMOOCOtOOCOtOOlCM CIOIOOOIOTOO-CM

00 o o* о o -

tOTflOCOlOCMCMCO-*001 COCOCMQOCOtOCMlOtOlO

о о о о о о о о о* о о

cOCOOilOlOlOCOtD-COTfCO QOCOt-TftDCOO-<СМСО COlOtOtOttb-tCOCOOOOO

000000000000

OtOOCOOlTfOllOOlOOO OOTfCOCO-TfintCOOOlOl

OJTfliOlOtDtDtOtDtDtOtOtO

о o о о o o o* o o* o o o

ttOlOOrftOCOddOOO -С0тЮЮЮЮЮЮ01ОСО

oooooooooooo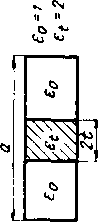

-(NOt-tt--CO<X>(OCO

00000000000

- COlOlO(Na>-00-.(N-

ю(осмц:?010(мссососо ooooooooo oo*

ocoOTftoi(Ni:Mcoco

CSCO--TfTflOlOlOiniO

0000000 00* 00*

tOtOTfCOCNOCOOlO TfOCOCOtOOlCMCOTfTi* COCOTfTflOlOlOirOlO

о о о о о о o* o o o o*

(ОЬ*тГ-<* 00сОтр-<* СЧСОттЮЮЮЮЮ

oooooooooo

Р1Р!5С1<1лоюоюоюо

---C4C4COCO-4jTtlOlOtOtOltXjCO<J)010

00000 о о о о* о о о о о* о сГ о* о -