- С4 М

СО СО СО

чГ

ОСОСОСЦЭСОО

юотгга> - мсо о - - - - cNCe

о ее

oooocicnoooo - - - соеоеосотртртр-чГ.,-.,!

оо о

оо СП .

со 1Л со

Saooeoeo-соооаося corroooooooooaoj сосоеоеососоооеоеососососо

S Ef S в

со ю

юососоюогсй - e>i(Ne>i toooo- саео--юююиэсоююю

CoieocoeocoeoeoeoeocOeoeococoeo

oiociioro - юог С-ООЮЮОООСО со lOOOtOOOO Ю - ЮаоСОт1*Юсо ССООСтрЮГООоООООО - - - -

CccctNoJcieoeoeoeocoeoeoco

oooooooeor Oicococn - io-rt*oo сО-соаог:- locooojiocor-f-CT(MiOr-oooo~-ojojojeoeop5eoco

о - - - CeOJOJCC4c5c4cJcJ

(>io-OitM- CO ->r-io(Neooo lOtp-O - - oo-oojioroooo

rOtNiOCOcOr- rOOOOtJOoOOO

COCTj*tC)C4Tj*C4QOTj* coooojojofooeOTfio toooooo - - - -

oooo - - -Г - - -

g* Ю CI

о о о о

SCOObOCTftOoOOOJ-4 tOOOO,. , оо - - - - - CtNC>iC4C4eoooeicoeo

ооооооооо о о ОООООООООООО

MetpoE заполнения t/a и ги С ростом t/a и а/к дисперсия уменьшается, а коэффициент замедления приближается

к величине eu т. е. характер распространения волн в этом случае во многом напоминает распространение в безграничном пространстве с относительной диэлектрической проницаемостью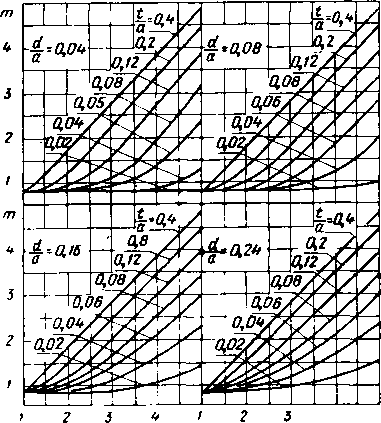

Рис. VI.6. Зависимость коэффициента замедления т от Kt при различных значениях tja и dja для аА=0.8.

Для ориентировочного определения коэффициента замедления При промежуточных значениях в интервале 8=1-25 можно 1пользоваться трафиками рис. VL6-

VI. 10, на которых даны зависимости т от YTt при различных геометрических размерах волноводно-диэлектри-ческой структуры. Характерной, особенностью этих кривых является линейный участок изменения т в зависимости

от let при достаточно большом заполнении волновода диэлектриком (/а>0,2).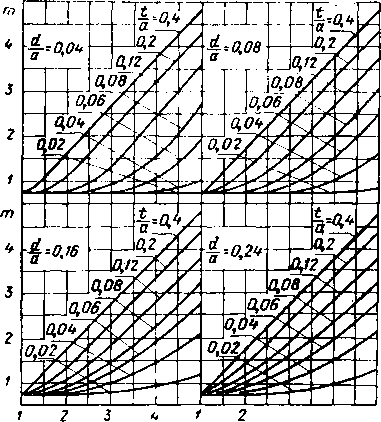

5 ,и

Рис. VI.7. Зависимость коэффициента замедления т от при

различных значениях tIa и dja для ajXJ.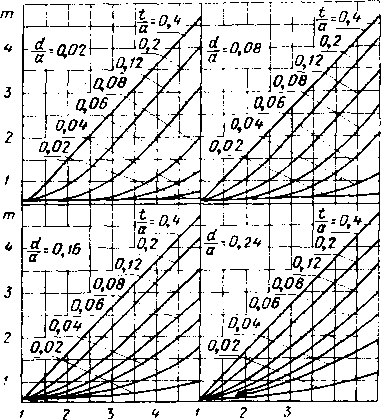

vet

Рис. VI.8. Зависимость коэффициента замедления m от ]Ге< при различных значениях ija и dja для ajk=Ofi.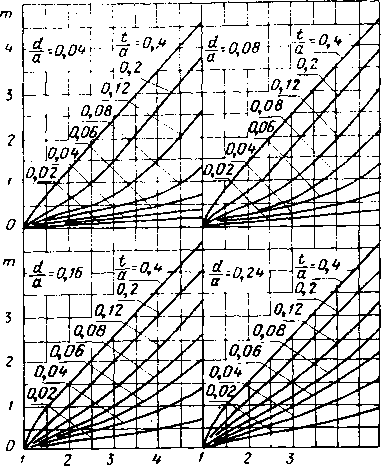

Рнс. VI.9. Зависимость коэффициента замедления т от Yпри различных значениях tfa и rf/a для а/х-оъ.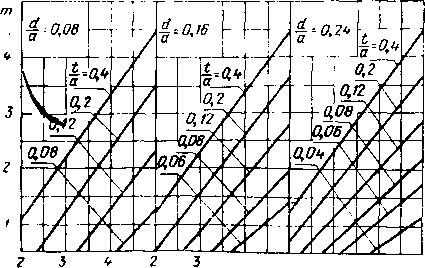

2 3 Ve;

Рис. VI.10. Зависимость коэффициента замедления т от Y7i при

l)M:(.(j[i4iir>ix лпачсги-£ЯА i/ и dja для а/х -о 4

16-1181 241

1ш Критические длины воли

Уравнение для определения критических размеров волновода с одной несимметрично расположенной диэлектрической пластиной получаем из дисперсионного уравнения (1.4), полагая коэффициент замедления равным нулю. В этом случае оно приобретает вид:

(VI.1)

Уравнение (VI.I) имеет бесчисленное множество корней, каждый из которых в порядке возра1стания соответствует более высокому типу колебаний. Практический интерес представляет наименьший корень, соответствующий основной Гю-волне (аДкрО, и корень аДкрг, соответствующий 7£2о-волне.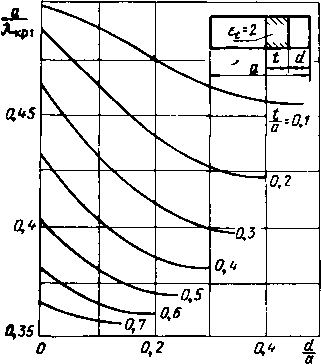

Рис. VLll. Нормированный критический размер аДкр! основной волны как функция положения пластины d/a при различных ifa

и Et=2.

На рис. VI.11-VI.15 представлены зависимости отношения ширины волновода к критической длине волны основного типа колебаний от положения диэлектрика d/a при различных значениях заполнения \t/a .и величине диэлектрической (Проницаемости =2, 4, 9, 16, 25. Характерной особенностью графиков является уменьшение?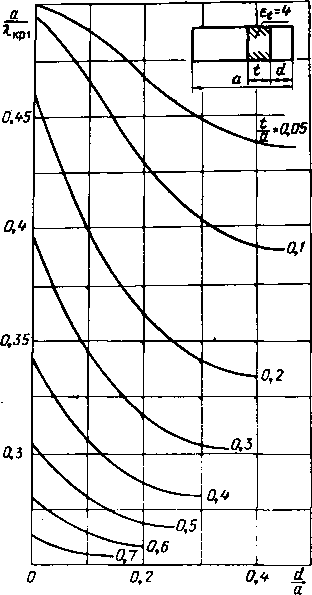

Рис. V.I2. Нормированный критический размер аДрк1 основной волны как функция положения пластины d/a при различных t/a и

е,=4.

йДкр! с увеличением d/a, т. е. с (приближением .пластины к центру волновода. Это объясняется эффектом усиления концентрации поля в пластине (( втягивание поля) при смещении ее к центру волновода, где напряженность по ля волны основного типа колебаний максимальна, В ре-

16* 243