стенки прямоугольного волновода, при котором возмож но распространение основного типа колебаний. Уменьшение ширины волновода тем больше, чем больше диэлектрическая проницаемость заполняющего диэлектрика. Обращает на себя внимание тот факт, что норми-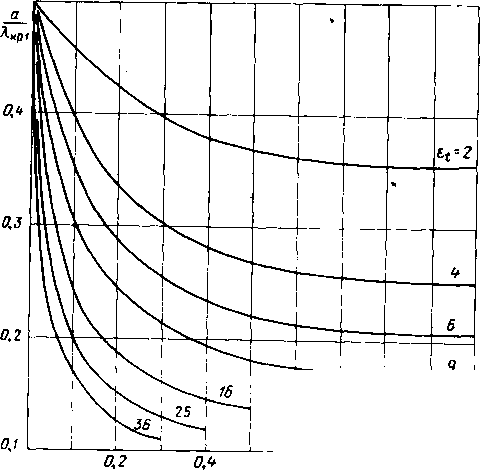

Рис. ПЛ. Нормированный критический размер alKvx основной волны как функция Itfa при различных 8*.

рованная к критической длине волны ширина волновода в зависимости от заполнения наиболее резко изменяется при малых заполнениях (2 а0,20) и почти не изменяется при больших заполнениях. Такая зависимость при малых заполнениях объясняется тем, что диэлектрическая пластина располагается в месте максимальной напряженности электрического поля в волноводе, где наиболее сильно проявляется эффект концентрации поля диэлектриком; при больших заполнениях все поле заключено в диэлектрике и дальнейшее увеличение размеров диэлектрика не может привести к существенно большей концентрации.

Ближайшей к основной волне является четная Г/Гго-волна. Полагая, как и для нечетных типов колебаний, коэффициент замедления в дисперсионном уравнении (II.2) равным нулю, получаем уравнение для критических длин волн четных типов колебаний

(11.4)

На рис. II.2 приведена зависимость корней а/Хкрз уравнения (II.4) для ГБго-волн от заполнения для значений диэлектрических проницаемостей заполняющего волновод диэлектрика 8/ = 2, 4, 6, 9, 16, 25 и 36,

Рис. II.2. Нормированный критический размер оДкрз первого высшего типа колебаний ТЕ как функция заполнения при различных £(.

Можно видеть, что кривые рис, II.2 отличаются от кривых рис. II.1, в основном, при малых заполнениях волновода (2 а0,20). В самом деле, при малых заполнениях в центре волновода при четном типе колебаний располагается узел напряженности электрического поля -и концентрация поля в диэлектрике проявляется слабо. При дальнейшем росте заполнения концентрация \\опь\ начнмае! пр(яьля1ьгя заметнее.

Таким образом, диэлектрическая пластина, расширяя полосу пропускания основного нечетного типа колебаний, не улучшает условия распространения ближайшего (четного) высшего типа колебаний, а наоборот, препятствует его возникновению. Если используя рис. II.1 и 11,2, построить зависимость отношения ЯкргАкр! от заполнения, то можно убедиться, что при всех заполнениях это отношение больше двух. В этом заключается одно из преимуществ частично заполненного волновода с центральной симметричной дилектриче-ской пластиной.

3. Характеристическое сопротивление

Для инженерных расчетов соединения волноводных линий передачи, различающихся по поперечному сечению и заполняющему диэлектрику, весьма плодотворным оказалось понятие характеристического сопротивления. Наиболее часто применяют определение характеристического сопротивления через напряжение бегущей волны в волноводе и передаваемую мощность (9-11];

(II.5)

напряжение, вычисляемое как

где V

грал от максимальной напряженности поля в волноводе;

линейный инте-электрического

Edx:=b Е

мощность, передаваемая по волноводу.

Используя граничные условия и проводя нормировку амплитуд, из выражений (1.5) -(1.7) получаем

E cos<f--x) при d<:x<Cd-j-2t.

(II.6)

где Л =rD

cos sin

cos и

** sin ad

Интегрируя no поперечному сечению и полагая в дальнейшем всюду относительную магнитную проницаемость диэлектрика равной единице, получаем для мощности, передаваемой по волноводу,

2/ /

sin 26/

EyHx*dxdy

аЪ т.

(II.7)

+ 1-

sin2a\ 2ad J

волно-

а, b - размеры прямоугольного волновода; х\ вое сопротивление свободного пространства, равное 377 ом.

Из выражений (П.5) и (П.7) находим характеристическое сопротивление

(II.8)

При отсутствии диэлектрика, так же как и при заполнении всего волновода диэлектриком, формула (II.8) переходит в известное соотношение [11

2t{a-\\

В табл. II.6-11.10 приведены данные расчета характеристического сопротивления, умноженного на ajb, по формуле (II.8) при заполнении волновода материалами с диэлектрическими проницаемостями Рг==2, 4, 9, 16 и 25. Расчеты проведены для основной волны. Отметим несколько особенностей этих таблиц.

С ростом диэлектрической проницаемости и заполнения хйрактристическое сопротивление частично заполненного волновода уменьшается и его значение убывает

примерно пропорционально

При малых значениях диэлектрических проницаемо-стей и определенных величинах заполнения наблюдается равенство характеристических сопротивлений незаполненного и частично заполненного волноводов. Однако в этих точках согласование незаполненного волновода с частично заполненным может быть осуществлено только при устранении реактивности в месте стыка соединяемых волноводов.

Данные расчета характеристического сопротивления

Характернстнческсе сопротивление, умноженное на безразмерный козффициент а/Ь. а/з Zpy. ом

0.025 0,050

0.075

0,100

0,125

0,150

0,20Г) 0,250

0,300

0,350

0,20

0,25

0.30

0,35

0.40

0,45

0.50 fi,55 п. GO 0.65 0,70 0.75 0,80 0.85 0,90 (-.95 1,00

0,400

0,5Э0

0,600

0,700

3433

1639

1307

1158

1074

1020

984,9

960.5

943,6

932,0

924,5

3077

1497

1217

1099

1040

1007

991,1

986,0

990,0

996,4

1008

1025

0,900

2014

1319

1123

103Г)

988.9

965.4

960,0

954,1

959,0

968,

981 ,9

998,0

1625

1194

1047

976.5

939,9

922,4

913,8

913,8

918.9

927,9

939,8

954,0

1409

1101

982.9 924.4 893.5 877,4 870.8 870.6 874.7 882,1 891,9 903,5

2758

1266

1028

928,6

877.7

850.1

835,5

829,0

827,9

830,6

836,1

843,7

852,7

2044

1165

968,5 882,2 836.7 811.0 796.8 789,8 787,7 788,9 792,5 798,0 804,7

1529

1030

в80,3 811,3 769,4 745,6 731,2 722.7 718,3 716,6 717,0 718,9 722,0

1317

947,9

821,3

757,6

720,4

696.9

681,6

671,6

665.1

661,0

658,8

658,0

658,3

1212

899.1

783,8 723,8 687,5 663,9 647,5 636,1 627,8 621,9 617,6 614,7 612.8

1143

863.3

790,0

697,2

661,1

636,6

619.0

605,9

595.9

587,9

581,5

576.4

572.0

Таблица 11.7

Данные расчета характеристического сопротивления

Характеристическое сопротивление, умноженное на безразмерный коэффициент ajb, ale Zpy, ом

0.025

0.050

0.075

0.100

0,125

0,15

0,20

0.25

0,30

0,35

0.40

0.45

0,50

0,55

0.60

0,65

0.70

0,75

0,80

0,85

0,90

0,95

1,00

2053 1429 1226 1127 1073 1042 1026 1020 1021 1027 1038