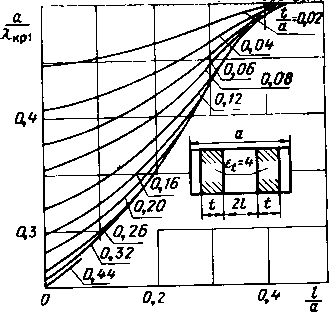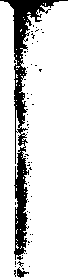Рис. v.l2. Нормированный критический размер аДкр1 основной волны как функция положения пластины а при различных tfa и 8=4.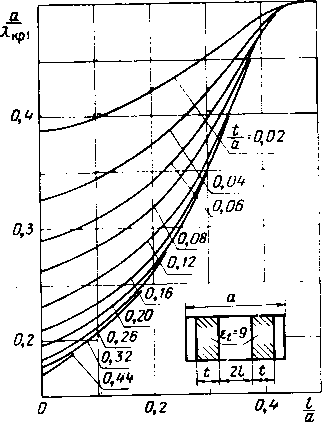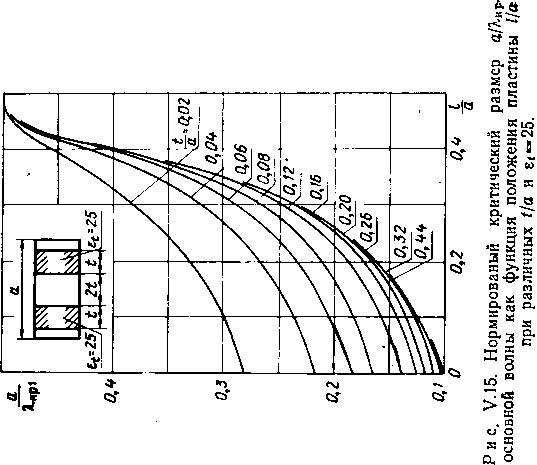

Рис. V.13. Нормированный критический размер аДцр1 основной волны как функция положения пластины l/a при различных t/a и 8 = 9.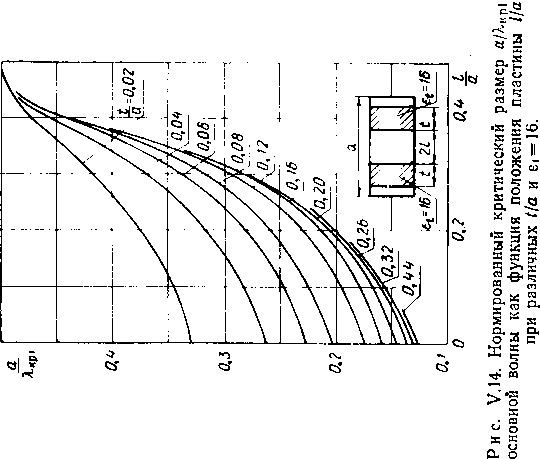

Тих данных путем уДвоейия размера а можно inojiyqktb значения критических длин волн для четных типов TEzo и ТЕш колебаний в волноводе с двумя диэлектрическими пластинами.

Отметим, что при небольших 1/а создаются более благоприятные условия для распространения нечетных типов волн по сравнению с четными типами волн. (Аналогичная ситуация уже встречалась при анализе волновода с одной центрально расположенной пластиной ib гл. II.) Это можно иллюстрировать на следующем примере: волновод с параметрами 8=9, а=0,04, /а=0,1 согласно графикам рис. V.13 характеризуется отношением аДкр1= = 0,25. При распространении четного типа ТЕо достаточно рассматривать волновод половинной ширины с одной Пластиной. Он имеет параметры t/a=0,2 и d/a=0,08, и согласно рис. VI. 13 а7кр1 = 0,315. Тогда исходный волноводна волне типа ТЕ20 будет иметь отношение аДкр2= = 0,63, т. е. WW=2,54.

Как известно, отношение Я.кр1Дкр2 для незаполненного волновода равно 2. Таким образом, симметричное затхол-пение прямоугольного волновода двумя диэлектрическими (Пластинами расширяет диапазон частот, в котором возможно распространение основной волны при отсутствии волн высших типов, и одновременно допускает уменьшение поперечных размеров. При больших l/a, когда шла-стины находятся вблизи узких стенок, выигрыша в широ-кополосности нет, и ситуация во многом напоминает волновод с двумя лластинами, прилегающими к узким стенкам (см. гл. III).

3. Затухание, обусловленное потерями в заполняющем диэлектрике

Проведем расчет затухания с ломощью метода малых возмущений [25]. Под возмущающим параметром подразумевается мнимая часть диэлектрической проницаемости материала пластины. Этот метод сводится к выделению мнимой части постоянной распространения ад из разложения ее в ряд по степеням мнимой части диэлектрической проницаемости г\. Так как для большинства СВЧ диэлектриков вещественная часть Е>>е

то в этом разложении можно ограничиться (первым членом

27ref dm

igb.

(V.2)

Производная dm/dsU вычисляется в предположении отсутствия потерь. Согласно оценкам 25] при б<<0,1 е.* погрешность расчета таким способом не превышает 3%, что вполне допустимо иа практике. Значение дт/дгг может быть рассчитано строго из уравнения \(1.10) после его дифференцирования как неявной функции. Однако для большинства практических приложений вполне достаточную точность дает оценка drnfdeU из графиков рис. V.6-V.10. Для ускорения расчетов целесообразно

использовать очевидное соотношение -~г- =--г=- X

X-гт=г Производная дт1д{У et) рассчитывается из приведенных графиков непосредственно.

В качестве tipHMcpa определим диэлектрические потери в прямоугольном волноводе с двумя Пластинами с параметрами аД=0,6; i/a = 0,16; /а = 0,06; ег=9; 1=10 см; тангенс угла диэлектрических потерь tg6=e/e = 10~.

По графику рис. V8 производная т/<?е( =0,082, что соответствует согласно (V.2) потерям 0,408 дб/м. Анализ локазал, что расхождение между значениями потерь, полученными строго и лриближенно, невелико. В данном случае оно не превышает 3%.

Глава VI

ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД

С НЕСИММЕТРИЧНО РАСПОЛОЖЕННОЙ

ДИЭЛЕКТРИЧЕСКОЙ ПЛАСТИНОЙ

1. Коэффициент замедления

Прямоугольный волновод с несимметрично расположенной диэлектрической пластиной (см. рис. 1.1,г) рассматривался в ряде работ [23, 24, 26-28]. Там же можно найти отдельные результаты расчета конкретных параметров данной структуры.

Основой для определения коэффициента замедления является уравнение (1Л). В табл. VT.1-VI.5 даны расчетные значения коэффициента замедления основной волны при различных положениях пла1стины d/a и заполнениях t/a для ряда значений нормированной ширины волновода а/К и диэлектрической проницаемости е<==2, 4, 9, 16 и 25.

Рассматриваемая волноводно-диэлектрическая структура в пределе при d->0 переходит в структуру, описанную в гл. ly. Поэтому с целью получения дополнительной информации В предельном случае дискретность изменения параметра i/a выбрана отличной от дискретности, используемой ib гл. IV. Кроме того, здесь приводятся коэффициенты замедления основной волны в областях, где могут рашространяться и )Волны Высших типов, тогда как в гл. IV эти коэффициенты даны лишь в области существования основной волны.

Из табл. VI.1-VI.5 видно, что .смещение пластины к центру волновода, т. е. увеличение d/a приводит к росту коэффициента замедления. Аналогичная картина имеет место н при увеличении относительного размера

пластины i/a. Оба эти эффекта объясняются ростом концентрации поля в пластине: в парвом случае за счет перемещения ее в область большей напряженности электрического поля, во ©тором-за счет увеличения ее относительных размеров. Порядок использования таблиц ничем не отличается от рассмотренного выше случая гл. V,§ 1.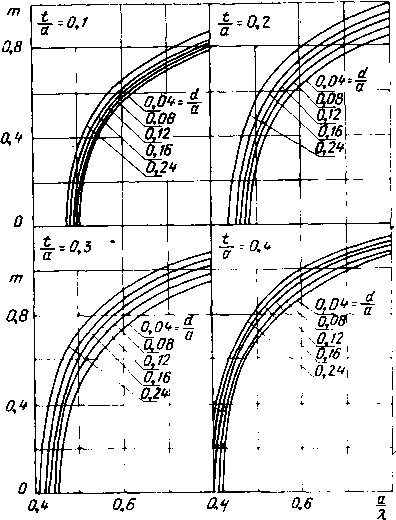

Р н С. VI.1. Зависимость коэффициента замедления т от нормированной ujHpHHjji волновода а/Х при различных значениях t/a и dja

для £( = 2.

На практике может потребоваться информация о коэффициенте замедления при значениях нормированной ширины волновода аД, отличной от тех, которые использованы в табл. VI. 1-VI.5. В этом случае полезны рис. VI.1-VI.5, на которых представлены зависимости коэффициента замедления т от о/Х при различных значениях геометрических размеров структуры и величине