
 |
|
|
Главная -> Диэлектрические волноводы Данные расчета коэффициента замедления Коэффициент замедления, т 2t}a 0,025 0,050 0,076 0,100 0,125
0.15 0,20 0,25 0,30 0.35 0,40 0,45 0,50 0,55 0.60 0.65 0.70 0.75 0.80 0,85 0,90 0,95 1.00
0.225 0,474 0.597 0,678 0,736 0,779 0.813 0.840 0.862 0,880 0,896 0,319 0,525 0,639 0,715 0,771 0,813 0.845 О 872 0,893 0.911 0.927 0,392 0.573 0,679 0.752 0.805 0,846 0.878 0.904 0.925 0.943 0,958 Et -2 0.-453 0,617 0.717 0,787 0,838 0.878 0,909 0,935 0,956 0.974 0,989 0.507 0,658 0,753 0.820 0.870 0,908 0,939 0,964 0.986 1.001 1.019 0,15 0.20 0,25 0.30 0,35 0,40 0.45 0,50 0,55 0,60 0,65 0.70 0,75 0,80 0.85 0,90 0,95 1,00  Данные расчета коэффициента замедления Таблица II. Коэффициент замедления, т 0,025 0.050 0,075 0,100 0,125 0.394 0,574 0,681 0.753 0.806 0,847 0.879 0.906 0,927 0,945 0.961
Данные расчета коэффициента замедления Коэффициент замедления, т 2t}a
0.350 0.400 0.500 0.600 0,700 0.900 1,549 1,937 2,151 2,292 2,393 2,471 2,533 2.585 2,627 2,664 2,695 2,722 2,746 2.767
f 9 Данные расчета коэффициента замедления Таблица 11.4 Коэффициент замедления, тп 2tla
0,200 1.091 1,947 2.329 2.573 2.753 2,896 3,015 3.116 3,202 3.277 3,341 3,398 3.448 3.491 3,530 3,565 3.596 0,250 0.300 1.617 2,291 2.629 2,849 3.010 3.137 3.240 3.326 3,398 3,459 3,511 3.556 3,596 3,630 3.660 0,350 0.400 0,500 0.600 0,700 1,970 2,552 2,856 3.054 3.198 3,309 3.397 3.470 3,530 3.580 3,623 3,660 3,691
0.900
го го Cf X & & Я) О ЕГ CJ о 2 X я (d Я S о ео (>J со оо о сч о t-- - t-- со ю t-- о со о со о сч - г со со со о о о LO Ю - со ю со ю со cr> о о оо (м со Lo со о LO CD со со 1ЛООО-ОСЦЮ rCOCOOOCDICO Г--СГ>ОСЧСО1ЛСГ> (MCOrfrf-rfrfrf сцюст)оооосоа;сосо OOtMCOQOLOOtLO- rfrfOOOCNCOrfLCD (NcOCO-rfrfrfrf 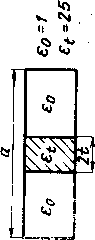 COrfCOrfOC-СОСЧ-< О-ЮОООССО-гУЮсО (NCOCOcOrf-rfrfrfrt 1Л1--.00ОООСЧО00-СЧС01--COCNCOt--COt--OOcr>OLO£31 LOOOCOCDOOO-CNCOrfLLOLO -CNCOCOCOrtrt rt:f:frt С01--.ООсГ>-000001--.--0 OJ OtLOOlOLOOrf-rfOOOcO СОСООСОЮГ--00-CNCOCO LO LO о < СЧ CO CO CO CO -iiOcDrfcOOCOcOCMCNcOLO о 00 CD LO CD CNCNCCOJCNCOCOCOCO CO CO CO OcDGOCO-rtt--.LOtDcO - CO о CO rfCLOCOOO-COlOtDttt CD Ю CO OrftDOOO-CCO-utDt--. 00 СУ) О CN(>J(NCN(NM(N СсЧ CO* CT3LOOO(MlO>fMCD-Ot--C4 - LO t--cO(NCi:>cDiO(NOt--COO cD CO О LocT3cNcorty:)OcDt--.Go 00 oi о ЮOlOOlOOlOOLOOlЛOЮOЮ - C4CNcOcO iOiOCOUt--.t--.GOOO
С ростом значения диэлектрической проницаемости растет коэффициент замедления, его значения приближаются к yet, С ростом величины заполнения и диэлектрической проницаемости уменьшаются значения а/Ху при которых возможно распространение основной волны в частично заполненном волноводе. При значениях диэлектрической проницаемости 8 = = 2 и 4 (табл. 11.1 и II.2) возможно такое заполнение {2t/a), при котором в значительном интервале изменений а/% коэффициент замедления близок к единице. Это означает, что в данном случае частично заполненный волновод оказывается линией передачи без дисперсии, где длина волны в волноводе равна длине волны в свободном пространстве. При больших значениях диэлектрической проницаемости (табл. II.4 и П.5) в значительном интервале изменений а/Х и 2t/a коэффициент замедления мало изменяется, это заметно при значениях диэлектрической проницаемости, больших девяти. Отметим, что в таблицах значения коэффициента замедления не приводятся, когда размеры волновода и диэлектрического заполнения допускают существование высших типов колебаний. 2. Критические длины волн Уравнение для определения критических длин волн легко получаем, полагая в дисперсионном уравнении (II.1) коэффициент замедления равным нулю. Тогда уравнение для критических длин волн нечетных типов колебаний принимает вид а yj (II.3) На рис. II.1 приведены графики зависимостей ширины волновода, нормированной к критической длине волны для первого нечетного типа колебаний, от величины заполнения. Можно видеть, как существенно уменьшается при заполнении диэлектриком размер широкой
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||