0,025

0Л50

0,075

0,100

0,125

0.150

0.200

0,250

0,300

0,350

0.400

0,500 0.600 0,700

0,15 0,20 0.25 0,30 0.35 0.40 0,45 0.50 0.55 0.60 0.65 0,70 0.75 0.80 0,85 0.90 0.95 1.00

0.418 0,554 0.640 0,701 0.746 0,782 0.808 0.832 0,851 0.866

0.424 0,827 1.082 1.293 1.480 1.643

0.537 1.031 1.331 1,562 1.751 1.907 2.037

0,374 1,110 1,463 1,713 1.907 2,060 2,183 2.283

1,026 1 .491 1,779 1.987 2.144 2.268 2,368

0.577 1,399 1.768 2.008 2,182 2,313 2.415

1,391 1.869 2.135 2,312 2,437 2.529

0.863 1,788 2.151 2.357 2.491

1.327 2.024 2.327 2,497

0,15 0,20 0,25 0,30 0,35 0.40 0,45 0.50 0,55 0,60 0.65 0.70 О 75 0.80 0.85 0.90 0.95 1.00

Продолжение табл. IV.I

Ко=?ффициент замедления, т

0,025

0,050 0,075 0.100 0,125

0,150

0,200

0,250

0.300

0.350

0,400

0,500

0,600

0.418 0,554 0,640 0,701 0,746 0,782 0,810 0,832 0,851 0,868

0,434 0,566 0.651 0.712 0,757 0,793 0,821 0,844 0.865

0.241 0,487 0,615 0.701 0,766 0,821 0,876

0,435 0,640 0,785 0.927 1,093

0,449 0,771 1.027 1.290 1,551

0,466 0,933 1.282 1,601 1.884

0,967 1,488 1,882 2,198 2.449 2.652

1,188 1,785 2.196 2.504 2,740 2,922 3,089

1,073 1,865 2,329 2,652 2,890 3.069 3,208

1,729 2,322 2,696 2,955 3,143 3.285

1,160 2,166 2,649 2.954 3,166 3,318

2.076 2,722 3,066 3,283

1,082 2.560 3,052 3.314

0,700

1,748 2,854 3,25а

xo га

.s a:

о о.

-fi-

о m сч

- г --

со о

со оо со о оз

0100 -

О] со

О] Oi Ю о

оо о о

О] со а> О]

О] со со

lO <D t>- оо <

со о сч о

со 1Х> со -

о О] со со

1 Ю О] С75 о

о со со о

о Ю 00 -

CS со со со

0 1 со оо -

OJ Ю о со

01 - ю оо

оГ со со со

00 ю а> оо со Г:-

со о а> о г:г

со о to оз о

-г сч со со со со

со СЧ - 00 00 со со

т: оо - о о

со оо

-г сч сч со со со со

со СЧ о 00 <N 92

GO со СЧ о

t-- о <Г 00 -

о CS CS сч го

1Л со 1 оо

ю а> о со to - со -

сч сч

от СЧ СП

о о -

сч - о со

Ю - со Oi

со ю 1 оо а>

о о о о о

ООСПСО -ОС--;-- Tj.IC0CMr~-Ot TflOCOIIOOCOOO

осГо ooooo

rni - СЧОО(МОСОСЧЛ>

--ю-о-сосоюсо ю со 1 1 оо 00 оо оо

о о о о о* о о о о о

- g Й g Й S S S g S S !5 S S § S 8

оооооооо

оооооооо

в табл. IV. 1 приведены значения коэффициента замедления волны основного типа колебаний для диэлектрических проницаемостей 8 = 2, 4, 9, 16 и 25 материалов, заполняющих волновод.

При малых заполнениях коэффициент замедления почти не зависит от заполнения. С ростом заполнения величина коэффициента замедления возрастает. Значения коэффициента замедления не [приводятся в таблицах при больших величинах отношения а/К, когда волновод-но-диэлектрическая структура допускает распространение ГЕго-волны. При увеличении диэлектрической проницаемости область изменений а/Х, при которой возможно еще распространение только основного типа колебаний, заметно уменьшается.

Частотная зависимость коэффициента замедления в рассматриваемой структуре более сильная, чем в двyri предыдущих. При больших заполнениях (t/aOJO) частотная зависимость коэффициента замедления слабая, так как большая часть энергии передается по диэлектрику.

2. Критические длины волн

Уравнение для определения критических длин волн данной волноводной структуры можно получить, Пола-гая коэффициент замедления в дисперсионном уравнении (IV. 1) равным нулю. В этом случае

2 KsoFbo

(IV.2)

Уравнение (IV.2) имеет бесчисленное множество корней (i/Xnp, каждый из которых в порядке 1Возрастания соответствует более высокому типу колебаний.

На рис. IV. 1 изображены зависимости аДкр! для основного типа колебаний от заполнения волновода материалами с диэлектрическими проницаемостями Et = 2, 4, 9, 16, 25 и 36; на рис. IV.2 - аналогичные зависимости лДкр2 для первого высшего типа колебаний. Зависимости отношения дДкр! от величины заполнения не имеют особенностей.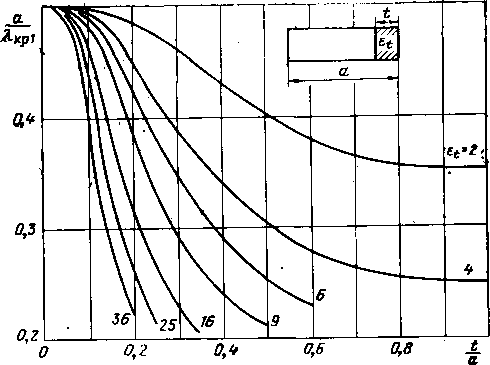

Рис, IV.l. Нормированный критический размер лД р1 основной волны как функция заполнения tja при различных 8/.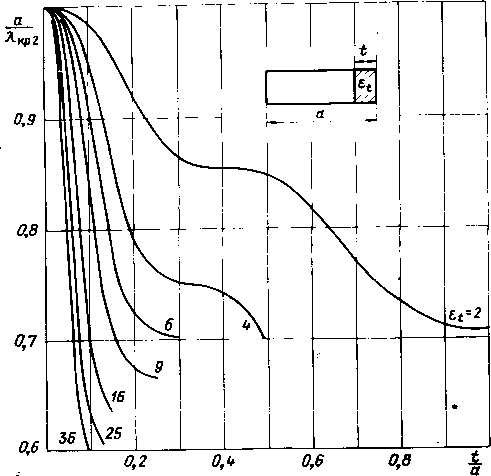

Рис. IV.2. Нормированный критический размер сДкрг первого высшего типа колебаний ТЕ20 как функция заполнения tja при различ

пых £(.

Характерной особенностью кривых, изображенных на рис. IV.2, являются участки, параллельные оси абсцисс. При заполнениях, соответствующих -плоской части кривой отношения А!/Лкр2, проявляется устойчивость данной структуры частично заполненного волновода к возбуждению Первого высшего типа колебаний.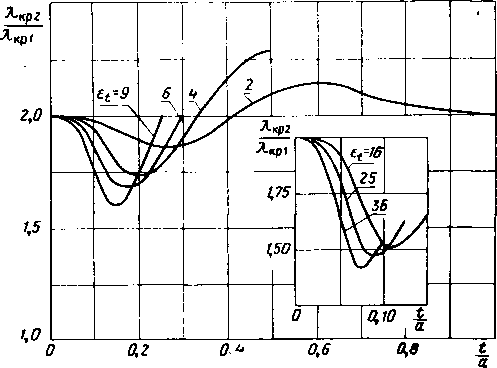

Рис. 1V.3. Зависимость отношения критических длин волн Л-краДкр! от заполнения tja при различных zt.

Если построить зависимость отношения Акрг/крГ от заполнения (рис. IV.3), то можно наблюдать, что это отношение принимает значения, меньшие и большие двух. Напомним, что отношение критической длины волны ближайшего высшего типа колебаний к критической длине волны основного типа колебаний (АргДкр!) при всех величинах заполнений для центрального симметричного расположения диэлектрической пластины всюду больше двух, а для симметричного расположения около боковых стенок всюду меньше двух. Таким образом, волновод с одной диэлектрической пластиной около боковой стенки является некоторой средней структурой по сравнению с волноводами, имеющими заполнение в виде одной центральной пластины или в виде двух -пластин, симметрично расположенных около боковых стенок.