являются более общими, чем структуры рис. 1.1,а, б, в. Последние можно получить, полагая в структурах рис. 1Л,г, д d=0 или /=0. Это позволяет ограничиться анализом общих структур.

Не останавливаясь на деталях вывода составляющих электромагнитных полей из дифференциальных уравнений, известных в литературе [1, 6, 20, 25], приведем лишь некоторые соотношения, которые потребуются нам в дальнейшем. Здесь и в дальнейшем предполагается зависимость от времени и координаты z в виде множителя е** *, который везде опускается.

Несимметричное расположение диэлектрической пластины в волноводе (рис. 1.1,г)

Составляющие электромагнитного, поля, удовлетворяющие граничным условиям, будут иметь вид:

- в области x<d (слева от диэлектрической пластины)

А sin ах,

Ях=--sin ах,

(1,1)

COS ах,

где a = -/efi.o - m\m=XlA - коэффициент замедления волны; X - длина волны в свободном пространстве; Г-постоянная распространения в волноводе; Л - длина волны в волноводе; ео, Цо - относительные значения диэлектрической и магнитной проницаемости свободного пространства;

- в области d+t<ix<ici (справа от диэлектрической пластины)

Еу = В sina (а - х),

- -- sm а (а - х).

(1.2)

Hz=--cos а (а - х)\

- В области dx<d-t (внутри диэлектрической пластины)

Еу = С sin {х - rf) + D cos р (х - d),

Ях = --[Csmp(x -rf) + Dcosp(x -d)], (1.3)

[С cos р (х - rf) - D sin р (х - d)].

где 8

ut - относительные значение диэлектрической и магнитной проницаемостей пластины;

A,B,C,D - постоянные коэффициенты.

Приравнивая тангенциальные составляющие электрического и магнитного полей на границах раздела сред из выражений (1.1) - (1.3), получим систему четырех однородных уравнений. Исключая из этой системы постоянные коэффициенты, приходим к дисперсионному уравнению, из которого вычисляется постоянная распространения:

55octgp/(tga/ + tgarf) +5 -5tg ad tg а/-О, (1.4)

где l = a-d-t, 5o=a/fio, 5 = р/ц/.

Уравнение (1.4) не изменяется при замене / на d и наоборот, т. е. при перемещении пластин слева направо в симметричное относительно центра волновода положение.

Симметричное расположение двух диэлектрических пластин (рис, 1.1,д)

В этом случае составляющие электромагнитного поля, удовлетворяющие граничным условиям, будут иметь вид:

- в области x<Cd

Еу - А sin ах.

Я.= -

sm ах.

(1.5)

Hz =--COS ах;

- в области а - d<x<a

у - Bsina(a - х).

sin а (а - х), cos а (а - х);

(1.6)

- в области dt<x<:dt2l (между диэлектрическими пластинами)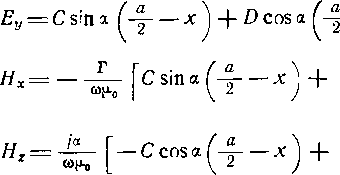

Dcosa---j

(1.7)

D cos а f -г--X

в области rf<.v<rf + (левая пластина) Яу = Р sin 8 (X - rf) + Q cos р (х - rf).

Р sin р (x - rf) + Q cos p (x - rf)], (1.8)

[P cosp(x -rf) -Qsinp(-\: -rf)];

- в области a - d - t<x<,a - d (правая пластина) = sin p (a - - д:) + S cos p (a - rf - x), Ях =--f? sin В ia-d - x) +S cos p (a-d- x)\. (1.9)

[ /cosp(a -rf --\:) + Ssinp(a -rf -X)].

Приравнивая тангенциальные составляющие, электрического и магнитного полей на границах раздела сред, из выражений (1.5) -(1.9) получаем систему восьми линейных однородных уравнений, из которой можно найти постоянные коэффициенты Л, В, С, D, Р, R, S. Исключая из этой системы коэффициенты, получим дис-

персионное уравнение в виде произведения двух сомножителей, которое распадается на два уравнения:

SSo Ctg р/ (tg ad - clg a/) + 5 tg ad clg al -ss, cig fit (tg ad + 1g al) - tg ad tg al

(1.10)

(1.11)

Можно показать i[25], что уравнение (I.IO) соответствует случаю С=0, А = В, Р=/?, Q=S, а уравнение (1.11) - случаю D==0, А --В, P = -R, Q = -S. Рассматривая поведение электрического поля в центре волновода при х=а/2, видим, что условию С=0 соответствует максимальное значение Еу, а условию D=0 соответствует Еу = 0, Таким образом, уравнение (1.10) описывает распространение нечетных типов волн Ггп+ю, а уравнение (1.11) -четных типов волн TEznO-

Уравнение (1.11) для четных типов волн прямоугольного волновода с двумя симметрично расположенными пластинами полностью совпадают с уравнением (1.4), описывающим распространение волн в волноводе с одной диэлектрической пластиной. Это совпадение объясняется тем, что поля Гпо-волн в структуре на рис. 1.1,2 аналогичны полям Ггпо-волн в левой или правой половине волновода (см. рис. 1.1,<3).

Таким образом, характеристики четных типов волн в волноводе с двумя симметрично расположенными пластинами идентичны характеристикам нечетных типов волн прямоугольного волновода с одной пластиной, имеющей относительное расположение, такое же, как в половине волновода с двумя пластинами.

Заметим, что дисперсионные уравнения (1.4), (1.10) и (1.11) могут быть получены на основе методов теорий цепей с использованием матричных представлений [7],

4. Техника вычислений

В следующих главах будут представлены данные расчета коэффициентов замедления и других характеристик различных волноводно-диэлектрических структур.

Коэффициенты замедления определялись из дисперсионных уравнений, которые для всех структур имеют трансцендентный вид. Вычисление коэффициентов замедления производилось методом хорд (последователь-

ная линейная интерполяция) на ЭВМ типа М-20. Значение корпя определялось с точностью до ±0,001. Выдача данных на печать производилась в виде массива чисел - корней в зависимости от интервала изменения параметра внутреннего цикла при фиксированном значении параметра внешнего цикла. При смене значения параметра внешнего цикла выдавался следующий массив. Такая форма выдачи данных удобна для контроля работы ЭВМ и отличается наглядностью. При составлении таблиц значения корней округлялись, что в ряде случаев приводило к дополнительному понижению точности вычисления корней на ±0,001. Таким образом, максимальная погрешность расчета корней дисперсионных уравнений не превышала ±0,002,

Диэлектрическая проницаемость большинства материалов, используемых в диапазоне СВЧ согласно данным § 1 (гл. I) лежит в пределах 1-25. Это определило диапазон изменения нормированной к длине волны ширины волновода, 0,15аД1,0. По ряду параметров использовался прогрессивный шаг изменения независимой переменной. Например, при малых заполнениях диэлектриком коэффициент замедления более чувствителен к степени заполнения, чем -при больших. В связи с этим значения корней в области малых заполнений рассчитываются при более мелком шаге по tfa, чем в области больших заполнений.

Структуры рис. 1.1,а, б, в, как уже отмечалось, могут в предельных случаях встретиться ори расчете более общих структур рис. 1.1,г, д. Чтобы избежать дублирования в счете, шаг изменения независимых переменных для этих типов структур выбран различным. Это одновременно дает дополнительную информацию по отдельным параметрам более простых структур и облегчает проведение интерполяционных процедур.

Глава II

ВОЛНОВОД с ЦЕНТРАЛЬНЫМ СИММЕТРИЧНЫМ РАСПОЛОЖЕНИЕМ ДИЭЛЕКТРИЧЕСКОЙ ПЛАСТИНЫ

1. Коэффициент замедления

Волноводно-диэлектрическая структура, изображенная на рис. 1.1,6, была подробно рассмотрена в литературе [8].

Составляющие лоля данной структуры для области x<id даются выражением (1.5), а для области d-\-2t< <x<a -выражением (1.6). Для области, занимаемой диэлектрической пластиной d<x<id-\-2t, составляющие поля можно легко получить из выражения (1.7), заменив поперечное волновое число а на ip и положив для нечетных типов колебаний С=0, а для четных - D=0.

Используя граничные условия или полагая в уравнениях (1.10) и (1Л1) /=0, после несложных преобразований для нечетных типов колебаний получаем

,[,-т Ctg (JtBtlit - m

а ) 1 -

2t \

а J \

(11.1)

а для четных типов колебаний

а 2t

(II.2)

В табл. ПЛ-II.5 приведены значения коэффициента замедления, при распространении основной волны, вычисленные из уравнения (ИЛ) для диэлектрических проницаемостей материалов 8 = 2, 4, 9, 15 и 25. Отметим несколько особенностей этих таблиц. 2-1181 17