
 |
|
|
Главная -> Диэлектрические волноводы Данные расчета коэффициента замедления 0.15 0.20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0.75 0,80 0,85 0,90 0,95 1.00 Коэффициент замедления т 0.000 0,025 0,050 0,075 0,100 0.125  0,150
 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0.50 0,55 0,60 0,65 0.70 0,75 0,80 0.85 0,90 0,95 1,00 Таблица III.3 Данные расчета коэффициента замедления Коэффициент заыедления, т 0,000 0,025 0,050 0,075 О.ШО
0,150 0,200 0,250 0,300 0.350 0,400 0,450 0.500
0.15 0,20 0.25 0,30 0,35 0.40 0.45 0,50 0.55 0,60 0.65 0,70 0,75 0.80 0,85 0,90 0,95 1.00 Данные расчета коэффициента замедления Коэффициент замедления, m 0.000 0,025 0,050 0,075 0,100 0.125
0,15 0.20 0.25 0.30 0.35 0,40 0.45 0,50 0.55 0,60 0.65 0.70 0.75 0,80 0.85 0.90 0,95 1.00 0,000 0,025 0.050  Та блица III.5 Данные расчета коэффициента замедления 0,075
Коэффициент замедления, m rf/a 0,100 0.125 0.150 0,200 0,250 0,300 0,350 0,400 0,450
0,869 1.732 2,287 2,744 3.116 3,411 3,643 3,828 3.978 0.819 2.020 2.624 3.075 3,427 3.690 3.909 4,072 2,009 2,764 3,235 3.583 3,847 4,049 1.310 2.745 3.311 3,670 3.931 4,128 2,343 3.318 3,745 4.009 4,196 3.077 3,818 4.138 4.321  0,500 3,727 4,330 4,583 4,714 2. Критические длины волн Уравнения для критических длин волн нечетных и четных типов колебаний получаем, полагая коэффициент замедления в дисперсионных уравнениях (III.1) и (IIL2) равным нулю. При этом уравнение для критических длин волн нечетных типов колебаний принимает вид tg ЫУТт 2d \ a J i 2d \ (III.3) a для четных типов колебаний 2d a tgUl/etfit 2d a (III.4) Ha (III.3) рис. III.I приведены найденные из уравнения зависимости отношения ширины волновода к критической длине волны основного типа от величины заполнения, а на рис. III.2 - найденные из уравнения (1П.4) зависимости отношения ширины волновода к критической длине волны первого высшего типа колебаний от величины заполнения. Из рисунков видно, что данная структура в отличие от центрального симметричного расположения диэлектрика не создает условий для преимущественного распространения основного типа колебаний. Ход зависимостей критических длин волн ог заполнения для основного и первого высшего типов колебаний примерно одинаков. Если, используя рис. III. 1 и III.2, построить зависимость отношения Якрг/Якр! от величины заполнения и диэлектричес-кой проницаемости, то можно легко убедиться, что это отношение меньше или равно двум. При этом с ростом значения диэлектрической проницаемости отношение ХкргДкр! уменьшается. Например, при диэлектрической проницаемости е( = 16 и заполнении d/a = 0,15 это отношение равно 1,3. Таким образом, заполнение волновода диэлектриком со стороны узких стенок уменьшает полосу пропускания 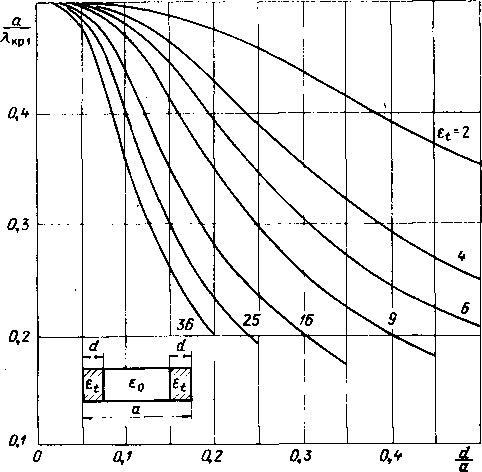 Рис. III.1. Нормированный критический размер а/Лкр! основной волны как функция заполиепия d/a при различных е. 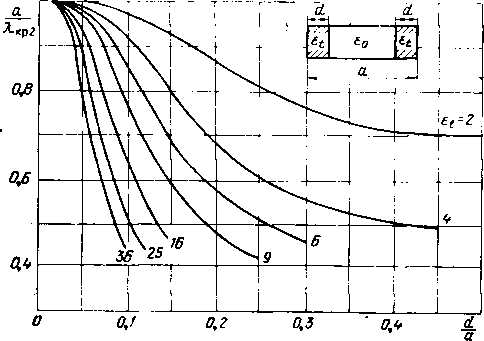 Рис. III.2. Нормированный критический размер аД р2 первого высшего типа колебаний TEsv, как функция заполнения при различных £(. 6-1181 81
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||