так как F (оо) = 1.

Формула (11.14) соответствует моменту нулевого порядка. Среднее значение (математическое ожидание) соответствует моменту первого порядка:

х= j xw{x)dx, (11.15)

- оо

что вытекает из формулы (11.5) как предел суммы. -

Моменты высших порядков по аналогии с (11.6) будут

а; = \ xw{x)dx. (11.16)

- оо

Таким же образом можно вычислить центральный момент т-го порядка

М[{х-х)]= J {x-x)w{x)dx. (11.17)

- оо

Как и в случае дискретных случайных величин, центральный момент первого порядка всегда равен нулю.

Рассеяние непрерывной случайной величины можно оценивать одним из следующих значений, словесные формулировки которых остаются прежними.

Среднее отклонение (мало удобная для вычислений величина)

+ 00

Д= J \x - x\w{x)dx. (11.18)

- оо

Дисперсия (наиболее удобная для вычислений величина)

+ 00

= J {x-x)w{x)dx = x-{x). (11.19)

Среднеквадратичное отклонение

а = УП = У х~{х). (11.20)

Средневероятньш отклонением называется такая величина, при которой отклонения а; - ж < Ад и \ х - х \ > имеют одинаковую вероятность.

Рассмотрим простейшие типовые законы распределения непрерьшных случайных величин.

Кроме того, имеет место зависимость

F{x)= w{x)dx. (11.13)

- оо

Вся площадь под кривой w (х) равна единице:

j w{x)dx==l, (11.14)

1. Равномерное распределение случайной величины на определенном участке характеризуется плотностью вероятности w {х) и функцией распределения F {х), показанными на рис. 11.9. При этом на основании свойства (11.14) имеем

Ъ-а

Подсчитаем характерные значения. Среднее значение (математическое ожидание)

+ 00 Ь

ж = j xw{x)dx= хс dx = .

Среднее значение квадрата случайной величины (момент второго порядка)

а;2= j xcdx= +а + 6

Дисперсия

Среднеквадратичное отклонение

а = У D =

к Ъ-а

2 уз

Рис. 11.9.

Средневероятное отклонение

Ав = 4-(Ь- )<о.

Максимально возможное отклонение случайной величины от среднего значения в данном случае будет

л Ь-

тах - 2

ЩЩ2. Нормальный закон распределения непрерывных случайных величин (закон Гаусса). Этот закон имеет вид

W (ж) :

(11.21)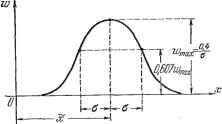

где о - среднеквадратичное отклонение, а X - математическое ожидание случайной величины.

График для этого закона изображен на рис. 11.10. Он имеет типичную колоколообразную форму.

Анализ условий возникновения нормального распределения показывает,

что оно имеет место во всех тех случаях, когда случайная величина характеризует собой суммарный эффект большого числа независимых причин. Поэтому нормальное распределение весьма часто встречается на практике. Для этого закона средневероятное отклонение будет

Рис. 11.10.

За максимальное отклонение, которое может иметь место, обычно принимают величину Ад1ах = За, так как вероятность того, что отклонение \ х - х \ будет больше Зо, очень мала, а именно:

Р {\х - X \ >-Зо) = 0,003.

Для удобства расчетов составлены таблицы для единичного нормального закона. Для получения этого закона положим ж = О и введем новую относительную переменную у = . Тогда вероятность того, что текущее значение

относительной переменной находится в интервале от -а до -\-а или сама переменная находится в интервале от -ао до +ао, определится выражением

(11.22)

Для функции Ф (а) составлены подробные таблицы. В качестве иллюстрации приводится краткая табл. 11.2.

Таблица 11.2-

Единичный нормальный закон

Рассмотрим пример пользования таблицей. Пусть имеется некоторая случайная величина х, для которой математическое ожидание ж = 10, а среднеквадратичное отклонение составляет о = 4. Определим, какова вероятность того, что случайная величина лежит в интервале 9,5 < ж < 10,5. Это означает, что отклонение от математического ожидания должно лежать в интервале -0,5 < А < -Н 0,5. Для относительных величин это соответствует неравенству

-0,125 <-<-f 0,125.

Таким образом, а = 0,125. По табл. 11.2 определяем путем интерполяции вероятность Ф {а) = 0,1.

Произведем более сложный расчет. Пусть для той же случайной величины необходимо определить вероятность нахождения ее в интервале 11 < а;-< 12. Так как кривая нормального распределения является симметричной относительно среднего значения случайной величины, то искомая вероятность может быть найдена как половина разности вероятности нахождения случайной величины в интервале -12 <Ц х <С 12 и вероятности нахождения в интервале -11 < а? < И, т. е.

а;<12) -Р(-11<а;<11)

ИЛИ для отклонений

Р(11<а;<12) =

Р(-2<Д<2)-Р(-1<Д<1)