D = (ж - ж)2 = {х - 2хх + = - 2хх -\-{xY=x~2 (х) -\r{xf=oi?-~ {xf,

т. е. она равна разности среднего квадрата и квадрата среднего значения случайной величины. Так как всегда выполняется неравенство >- {xf, то дисперсия может быть только положительным числом: D 0.

Корень квадратный из дисперсии называется среднеквадратичным отклонением случайной величины от среднего значения:

Для рассмотренного выше примера бросания игральной кости 6

Dy,{xi- xfPi = -i [(6 - 3,5)2 -Ь (5 - 3,5)2 + (4 - 3,5)2 -f

-Ь (3-3,5)2 + (2-3,5)2+(1 - 3,5)2] =11 = 2 g. Среднеквадратичное отклонение

a = lAZ) = / = l,7.

Укажем простейшие свойства среднеквадратичных отклонений.

1. При сложении независимых случайных величин

дисперсии складываются:

D = D + Dy + D,+ ...

Поэтому среднеквадратичное отклонение суммы независимых случайных величин

Ои = У(У1 + а1-\-о1+ ...

Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок.

2. Пусть имеется п случайных величин

17 -а З 4 ) п

С одинаковыми средними значениями а; и с одинаковыми законами распределения. Тогда их среднее арифметическое

тоже будет случайной величиной с тем же самым средним значением у =х, но среднеквадратичное отклонение его будет в раз меньше, чем для каждой из составляюш;их (в случае независимых случайных величин):

Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое, хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквадратичное отклонение), чем канодое измерение в отдельности. Здесь случайные ошибки измерения

Дисперсия может быть легко вычислена на основашш свойства среднего значения:

в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой массовостью измерений скомпенсированы быть не могут.

3. Для п случайных величин, независимых и имеюнщх одно и то же среднее значение х, среднее арифметическое будет при достаточно большом п как угодно мало отличаться от среднего значения х (с вероятностью, как угодно близкой к един1ще). Замечание в скобках означает, что это практически достоверно, но не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом п и указанных условиях

Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет первостепенное значение для обработки экспериментальных данных и для учетной статистики.

Введем теперь понятие интегрального закона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, меньшее некоторого значения х. Математически эта формулировка записывается в виде

F{x) = Р{1<Сх),

где - текущее значение случайной величины х. Например, если график закона распределения дискретной случайной величины х имеет вид, показанный на рис. 11.5, а, то график функции распределения F (ж) для нее будет иметь вид, показанный на рис. 11.5, б. Он показывает, что вероятность того, ffj что величина х получит значение мень-

ше единицы, равна нулю; меньше трех - равна 0,2; меньше четырех -

0,6-

2 3 4 S Рис. 11.5.

Б 7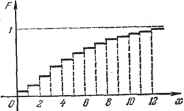

Рис. 11.6.

равна 0,6 и т. д. Функция распределения F (ж) всегда возрастает с увеличением X, причем F {х) = 1 при наибольшем возможном значении Хщах и остается равной единице при всех значениях х > .Гщах-

Например, для закона Пуассона (11.3), когда дискретная случайная величина может принимать значения .-г = О, 1, 2, 3, . . ., функция распределения

F(x) = Y,P(x) о

(11.10)

будет иметь вид бесконечной лестницы (рис. 11.6), но не заходящей выше единицы, т. е. F (х) 1 при х оо.

Вероятностные характеристики непрерывных случайных величин- Непрерывная случайная величина может принимать все значения в каком-либо заданном ограниченном интервале (а .г Ь) или все значения от -оо до +00. Следовательно, функция распределения (интегральный закон распределения) для непрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показаны оба упомянутых вьппе варианта.

Вероятность того, что непрерывная случайная величина примет определенное числовое значение х, бесконечно мала (например, вероятность попадания центра тяжести снаряда в определенную точку цели). Вероятность же того, что непрерывная случайная величина окажется в некотором промежутке xi<i х<Сх2, будет иметь конечное значение, а именно:

P{xi<l<C х) = F (х) - F (х).

Вероятность того, что непрерывная случайная величхша содержится в промежутке между X ш X + dx, будет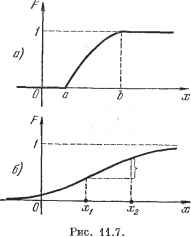

Р{х<.1<: x+dx) = dF {х) = dx.

Величина

= и;(.) (11.11)

называется плотностью вероятности. Закон распределения для непрерывной случайной величины в отличие от дискретной задается не в виде значений вероятности, а в виде плотности eepoflmuocmu w (х), называемой также дифференциальным законом распределения. На рис: 11.8 показаны дифференциальные законы распределения для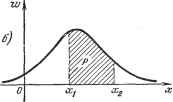

Рис. 11.8.

двух вариантов функции распределения F (х), показанных на рис. 11.7. Если бы здесь использовалось то же понятие закона распределения, что и для дискретной случайной величины, то получились бы бесконечно малые ординаты Р {х).

Выражение w (х) dx означает вероятность того, что случайная величина содержится между х в. х dx:

Р {х <Сй-< X + dx) = W {х) dx.

Вероятность того, что случайная величина содержится между значениями Xi и Xz, определяется формулой

P(xi<l<х) = j ы;{х) dx, (И.12)

что геометрически выражается заштрихованной. площадью на рис. 11.8.