режима, для чего в (10.3) необходимо положить р = 0:

W /0)---

(10.23)

Здесь может быть два случая. Если выполняется условие Woe (0) = 0> что будет при использовании в цепи обратной связи дифференцирующих элементов, то в установившемся режиме W, (0) = Wc (0). Это означает, что в этом режиме передаточная функция цепи, охваченной обратной связью, будет равна передаточной функции исходной цепи. Такая обратная связь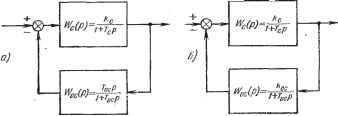

Рис. 10.9.

называется гибкой. Нетрудно видеть, что гибкая обратная связь действует только в переходных режимах, а в установившемся режиме она как бы отключается.

Если Woe (0) =Ф 0> то обратная связь действует не только в переходном, но и в установившемся режиме. В зтом случае обратная связь называется жесткой.

Заметим, что случай, когда звено, охватываемое обратной связью, относится к числу интегрирующих звеньев и Wc (0) -> оо не вносит особенностей. Здесь по-прежнему условие Woe (0) = О будет соответствовать случаю гибкой обратной связи, так как числитель (10.23) будет стремиться к бесконечности быстрее, чем знаменатель, и результирующая передаточная функция WcK (0) -> оо так же, как и передаточная функция исходной цепи. Заметим также, что понятие гибкой или жесткой обратной связи связано с той величиной, которая принимается в качестве выходной в исходном звене. Так, например, обратная связь может быть гибкой по отношению к углу поворота вала двигателя и жесткой по отношению к скорости его вращения, которая является первой производной от угла поворота.

На рис. 10.9, а и 10.9, б изображены примеры гибкой и жесткой отрицательных обратных связей. Обратной связью замыкается апериодическое звено с передаточной функцией

=() = 1W-

В первом случае (рис. 10.9, а) обратная связь представляет собой дифференцирующее звено с замедлением (например, дифференцирующий конденсатор) с передаточной функцией

Wocip)-

ТосР

1 + ГосР

Результирующая передаточная функция

(i+УосР)

Ч-Ис (р) Иос (р) 1+(гс+гос+!сгос) р+УсУоср

Результирующая передаточная функция

W (т,\ ip Mi±?WO

okW i + Wo{p)Woc{p) i + kckoo + (To + Toc)p+TcTooP

kc (l+TocP)

\i + кокос кокос

i +кокос

представляет собой новое значение коэффициента передачи звена, замкнутого обратной связью. В рассмотренном случае обратная связь является жесткой, так как она изменяет коэффициент передачи звена в установившемся состоянии.

Весьма важным является случай, когда цепь обратной связи представляет собой идеальное безьшерционное звено с передаточной функцией Woe ip) = ос- Этот случай легко получить из последних равенств, положив в них Too = 0. В результате для апериодического звена, замкнутого такой отрицательной обратной связью, получим

ко 1 кск

WcAp)

-i + klkoo ~Ц+кокос

Из этих выражений видно, что подобная отрицательная обратная связь уменьшает коэффициент передачи и постоянную времени апериодического звена в 1 -f- кокос раз, где кокос представляет собой коэффщиент передачи по петле обратной связи.

На первый взгляд здесь имеет место полная аналогия со случаем уменьшения постоянной времени и коэффициента передачи звена в одинаковое число раз при помощи пассивного дифференцирующего звена (см. § 10.2). Однако это не так. Если рассмотреть случай двух апериодических звеньев-первого порядка с , одинаковьши постоянными времени Т = = Tq, включенных последовательно, то, как нетрудно показать, для уменьшения суммы постоянных времени Т, + = 2То в п раз при помощи пассивных дифференцирующих звеньев необходимо подавить результирующий коэффициент передачи в раз. При решении этой же задачи посредством использования жесткой обратной связи, охватывающей сразу оба звена, получится снижение результирующего коэффициента передачи только в п раз. Задача снижения суммы постоянных времени звеньев, входящих в систему регулирования, встречается в практике довольно часто. Это делает применение обратных связей обычно более предпочтительньш.

В динамическом отношении отрицательные обратные связи могут оказывать самое различное действие. Однако, подобно тому как это было сделано

Результирующий коэффициент передачи в установившемся состоянии равен кс, так же как и в исходном апериодическом звене. Таким образом, эта обратная связь является гибкой. Наличие дифференцирующего элемента в цепи обратной связи и привело к получению гибкой обратной связи.

Во втором случае (рис. 10.9, б) обратная связь представляет собой апериодическое звено с передаточной функцией

ДЛЯ последовательных корректирующих устройств, можно наметить три основных вида отрицательных обратных связей:

1) обратные связи, подавляющие высокие частоты (аналоги пассивного последовательного интегрирующего звена);

2) обратные связи, подавляющие низкие частоты (аналоги пассивного последовательного дифференцирующего звена).

3) обратные связи, подавляющие средние частоты (аналоги пассивного последовательного хштегро-дифференцирующего звена);

Установить аналогию обратной связи с тем или иным последовательным корректирующим звеном можно при помогци формул перехода (10.5) и (10.6). Особенно важно иметь возможность перехода от последовательного корректирующего звена к эквивалентной обратной связи. Это определяется тем, что расчетным путем наиболее просто определить параметры последовательного корректирующего звена, а с точки зрения технического осуществления наиболее удобны обратные связи.

В табл. 10.4 приведены наиболее распространенные случаи перехода от электрических последовательных корректирующих звеньев к электрическим обратным связям. Эта таблица может быть использована также для перехода от последовательных звеньев к обратным связям любого типа (неэлектрическим), так как она позволяет по передаточной функции последовательного звена определить передаточную функцию эквивалентной отрицательной обратной связи.

Отрицательные обратные связи. Отрицательные корректирующие обратные связи очень часто используются для охвата исполнительных двигателей и серводвигателей (вспомогательных двшате-лей). В связи с этим рассмотрим наиболее важные случаи.

На рис. 10.10 изображено несколько случаев охвата электродвигателя отрицательной обратной связью. Схема на рис, 10.10, а соответствует использованию линейного потенциометра П, сцепленного через редуктор Р с валом двигателя Д. Напряжение, снимаемое с потенциометра, поступает на вход усилителя, от которого управляется двигатель. Пусть передаточная функция двигателя совместно с усилителем соответствует интегрирующему звену с замедлением:

(10,24)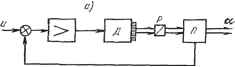

&= тг

НЬ>]->j д

Рис. 10.10.

тде - электромеханическая постоянная времени.

Передаточная функция цепи обратной связи Woo (р) - равна коэффициенту передачи потенциометра. Результирующая передаточная функция в соответствии с формулой (10.3) будет.

Wr.M- г--.2Лл, =J~..o.l....-, . (10.25)

W-fP+ кое l + Bgrp-t-yzpg

ккг.

2 УккпТм