Лрг/ЖШ/а

Релейные системы, так же как и дискретные цифровые (с двоичным-кодом), обладают перед непрерывными системами тем преимуществом, что-

не требуют высокой стабильности элементов для соблюдения определенной зависимости между выходной и входной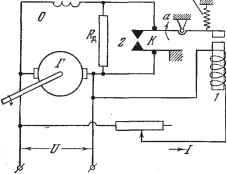

Рис. 1.41.

Рис. 1.42.

величинами. Они работают но принципу да - нет , т. е. но наличию или отсутствию входного сигнала и его знаку (с определенным порогом срабатывания).

ГЛАВА 2

ПРОГРАММЫ И ЗАКОНЫ РЕГУЛИРОВАНИЯ. АДАПТИВНЫЕ СИСТЕМЫ

§ 2.1. Программы регулирования

Задачей системы автоматического регулирования или управления является, как уже говорилось, поддержание требуемого значения регулируемой величины у (рис. 1.5) или изменение ее-но определенной программе, которая либо заранее задается, либо поступает извне во время эксплуатации системы в зависимости от некоторых условий.

Программы могут быть временными (задаваемыми во времени):

У = У it),

или параметрическими (задаваемыми в текущих координатах):

у = у (%, S2, . . ., Sr,),

тде Si, 2, . . ., Sn - какие-либо физические величины, характеризующие текущее состояние объекта в процессе регулирования.

Примером временной программы может служить программа изменения регулируемой величины, обеспечивающая правильный режим начального разгона мощного регулируемого объекта при пуске его в ход до наступления режима нормальной эксплуатации, в котором объект затем будет работать длительное время.

Например, автоматический регулятор угловой скорости мощного двигателя может быть предназначен не только для поддержания постоянной скорости в режиме нормальной эксплуатации, но еще и для регулирования требуемого режима нарастания скорости во времени (рис. 2.1, где у - угловая скорость) при пуске двигателя в ход, чтобы избежать каких-либо опасных отклонений.

Аналогичная программа регулирования во времени может задаваться при термической обработке металлов, когда требуется определенный режим быстроты нагревания металла (рис. 2.1, где у - температура в печи) до определенной температуры уд, при которой металл затем будет выдерживаться в печи.

В других случаях нормальный режим работы объекта может быть связан с непрерывным программным изменением регулируемой величины во времени (рис. 2.2), например угла тангажа вертикально взлетающей ракеты на активном участке ее полета [94].

Во всех описанных случаях в составе автоматического регулятора или системы управления имеется программное устройство (рис. 1.3), в которое заранее заложена требуемая временная программа. В случае же следящей системы тоже задается требуемый закон изменения регулируемой величины g (t) (рис. 1.5), но он не задан заранее, а может быть в определенных пределах произвольным.

Примером параметрической программы регулирования может служить задание требуемого неременного значения высоты полета у (рис. 2.3) при снижении летательного аппарата, но не во времени, а в зависимости от текущего значения пройденного пути s, чтобы снизиться в определенную точку независимо от времени протекания этого процесса.

Другим примером параметрической программы регулирования может быть задание неременного давления в герметической кабине высотного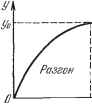

Нормальная \эмсплуатаиия

Рис. 2.1.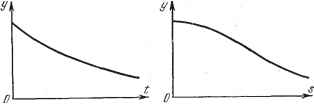

Рис, 2.2.

Рис. 2.3.

Рис. 2.4-

самолета в зависимости от текущего значения высоты полета (рис. 2.3, где у - давление, s - высота).

Наконец, типичным примером параметрических программ регулирования являются так называемые законы наведения в системах телеуправления и самонаведения снарядов. Законом наведения называется особая программа управления, которая задается через текущие значения координат и скоростей управляемого объекта независимо от того, в какой момент времени они имеют место в процессе движения объекта.

Пусть, например, тело А (рис. 2.4) должно быть сближено с телом В для мягкого контакта; р - текущее относительное расстояние между ними. Условия, которые должны быть выполнены в процессе сближения, следующие:

р <0, = О при р = О, р I ограничено, Т ограничено.

(2.1) (2.2)

(2.3) (2.4)

где Т - время сближения. Условие (2.2) - условие мягкого контакта в конце сближения. Условия (2.1), (2.3) должны выполняться в течение

всего процесса сближения, причем ограничение р связано с ограничением мощности или силы управляющего воздействия. Представим закон наведения в виде

Р + / (Р) = 0; (2.5)

аким образом, в системе регулирования должны быть измерители величин р и р и устройство формирования сигнала

и = Р + / (Р),

(2.6)

величина которого должна при помощи системы регулирования все время сводиться к нулю. Найдем целесообразное выражение функции / (р).