Подробнее расчет пассивных дифференцирующих звеньев на несущей частоте приведен в [27, 38].

Последовательные корректирующие звенья могут быть также построены на механических элементах. В табл. 10.3 изображены три основных пассивных звена: дифференцирующее, интегрирующее и интегро-дифференцирую-щее. Эти звенья построены на пружинах и демпферах. В качестве входной величины используется перемещение и выходной - перемещение х.

Таблица 10.3

Название и схема звена

Передаточная функция

Параметры

Дифференцирующее S

I-VWV-

т !? т Gj

Интегрирующее

1+у2р

l-biP

Ci-bC,

Интегро-дифференцирующее

Члллл-

(1 + у1р)(1-ьг2р)

а+ада+пр)

7-1 =

3,4=--9-

(l±/i

4Г,72

Передаточные функции этих звеньев полностью совпадают с передаточными функциями соответствующих звеньев, приведенных в табл. 10.1, для идеализированного случая (/?и О и i?b -> оо). Параметры элементов можно получить из приведенных в табл. 10.1 формул для электрических звеньев заменой емкостей конденсаторов (С) на коэффициенты сопротивления демпферов {S) и электрического сопротивления (i?) на величину, обратную жесткости пружины (с).

§ 10.3. Параллельные корректирующие звенья

Как уже отмечалось, параллельные корректирующие звенья удобно применять при использовании сложных законов управления, когда наряду с основным сигналом вводятся его производные или интегралы.

Введение интегралов преследует цель снижения установившейся ошибки. Этот вопрос был рассмотрен в главе 9 в связи с повышением точности систем

автоматического регулирования посредством использования изодромных устройств.

Введение производных преследует обычно цель обеспечения устойчивости. В этом случае используются звенья дифференцируюпего типа, включаемые параллельно основной цепи.

Варианты параллельного включения дифференцируюпих звеньев показаны на рис. 10.6. Получение производной второго порядка при помопи одного звена является затруднительным. Поэтому схема, изображенная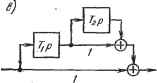

/0 Н р-{ Тгр -[

Рис. 10.6.

на рис. 10.6, б используется редко. Введение второй производной дополнительно к первой производной осуп;ествляется обычно по каскадньш схемам, изображенным на рис. 10.6, в и 10.6, г. Для первой из них (рис. 10.6, е) результируюпая передаточная функция будет

W(p) = 1 -Ь Tip-Ь а для второй (рис. 10.6, г)

W(p) = 1 -Ь (Г1 + Г,)р + fir

(10.18)

(10.19)

На рис. 10.6 дифференциаторы изображены идеальными. Более вероятно, что они будут представлять собой дифференцирующие звенья с замедлением (рис. 4.24).

Заметим, что введение параллельных корректирующих звеньев, представляющих собой интеграторы, соответствует поднятию .нижних частот. Это хорошо видно на рис. 9.6. Введение параллельных корректирующих звеньев, представляющих собой дифференциаторы, соответствует поднятию верхних частот. Это можно видеть из формул (10.18) и (10.19).

В качестве примера на рис. 10.7, а изображен случай введения дополнительно к основному сигналу, пропорциональному углу поворота вала, сигналов, пропорциональных первой и второй производным угла поворота. Первый сигнал вырабатывается датчиком угла - потенциометром, второй - тахогенератором и третий - дифференцирующим трансформатором, на вход которого поступает напряжение тахогенератора.

На рис. 10.7, б приведена структурная схема рассматриваемого устройства. На ней обозначено: - коэффициент передачи потенциометра, к -

коэффициент передачи тахогенератора, vs. Т - коэффициент передачи и постоянная времени дифференцирующего трансформатора. Результирующая передаточная функция

W{p)ki + k,p + .

(10.20)

Структурная схема может быть приведена к виду, изображенному на рис. 10.7, в, если в выражении (10.20) вынести за скобки множитель А:

(10.21)

где Г,=.

W(p) = k,[i + np+),

Структурная схема для этого случая приведена на рис. 10.7, в.

1+Тр

ОС

><зР

t+Tp

Рис. 10.7.

На рис. 10.8 приведен пример параллельного соединения гироскопических чувствительных элементов. Трехстепенный гироскоп Г-1 сохраняет заданное положение в простран-

ш Л:2

стве. Поэтому при наклоне основания на выходе потенциометра II-1 будет возникать напряжение, пропорциональное этому углу наклона: щ = к. Двухстепенный гироскоп Г-2 работает в режиме гиротахометра. При наклонах основания угол прецессии

его можно приближенно считать пропорциональным скорости наклона. На выходе потенциометра П-2 будет поэтому напряжение щ, = ка. Сумма напряжений и = щ определит результирующую передаточную функ-

Рис. 10.8.

W{p) = ki + h-

hii+Tp),

(10.22)

Этой передаточной функции соответствует структурная схема 10.6, а. § 10.4. Обратные связи

Как уже отмечалось выше, обратные связи (см. рис. 10.1, в) могут быть положительными и отрицательными. Кроме того, обратные связи могут быть жесткими и гибкими. Для уяснения последнего рассмотрим передаточную функцию (10.3), записанную для случая отрицательной обратной связи. Из этого выражения найдем передаточную функцию для установившегося