лов и производных от сигнала ошибки. Примером этому может служить рассмотренный в предыдущей главе случай использования йзодромных устройств.

Обратные связи находят наиболее широкое применение вследствие простоты технической реализации. Это объясняется тем обстоятельством, что на вход обратной связи поступает сигнал сравнительно высокого уровня, часто даже непосредственно с выхода системы регулирования, промежз-точно-го серводвигателя или выходного каскада усилителя. Другое не менее важное обстоятельство заключается в том, что корректирующие устройства различного типа оказывают различное влияние па содержащиеся в системе

I---i

I i

Рис. 10.2.

нелинейности. Если обратная связь охватывает участок канала регулирования, содержащий какую-либо нелинейность, например силы трения, люфт, зону нечувствительности и т. п., то влияние этой нелинейности на протекание процессов в системе регулирования меняется существенным образом. Отрицательные обратные связи имеют свойство уменьшать влияние нелинейностей тех участков цепи регулирования, которые ими охватываются. Так как практически все системы регулирования содержат те или иные нелинейности, ухудшающие качество регулирования, то использование корректирующих устройств в виде отрицательных обратных связей, как правило, дает возможность добиться лучших результатов по сравнению с другими типами корректирующих устройств.

Аналогичным образом отрицательные обратные связи дают значительно лучший эффект в тех случаях, когда вследствие воздействия внешних факторов (время, температура и т. п.) меняется коэффициент усиления какой-либо части цепи регулирования, охватываемой отрицательной обратной связью.

§ 10.2. Последовательные корректирующие звенья

Корректирующие звенья последовательного типа могут составляться из различных по своей физической природе эементов - электрических, механических, гидравлических и т. д. Наиболее просто такие звенья могут бьггь составлены из электрических С- и L-элементов. Электрические последовательные звенья имеют самое широкое распространение в системах автоматического регулирования, поэтому в дальнейшем они будут рассмотрены в первую очередь.

Последовательные звенья из С- и L-элементов часто называют пассив-1П.1МИ последовательными корректирующими устройствами, так как они не содержат источников электродвижущих сил.

Существует весьма большое количество пассивных последовательных звеньев. В некоторых книгах и справочниках приводятся таблицы, содержащие схемы десятков и даже сотен звеньев различного вида.

Обычно пассивные последовательные звенья могут быть представлены в виде обобщенной схемы, изображенной на рис. 10.3.

Функции (р) И (р) представляют собой сопротивления участков цепи, записанные в операторной форме. Влияние предыдущего и последующего звеньев на работу последовательного корректирующего звена может быть учтено введением сопротивления выхода источника сигнала i? и сопротивления входа i?B.

С учетом введенных сопротивлений передаточная функция последовательного звена будет

Двз (р)

(10.11)

W /пЬ-

Дв + 22(р)

Ди + 21(р) +

Двз (Р)

Дв+г (Р)

В идеализированном случае, когда приобретает вид

С2(Р) С2(Р)

О, а i?E оо, формула (10.11)

2 (Р)

Е{Р)

Ulip) Zi(p) + Z2{p)

(10.12)

Передаточная функция (10.11), как правило, соответствует звеньям с более плохими корректирующими свойствами по срав5аению с (10.12).

В табл. 10.1 приведены основные типы последовательных пассивных электрических корректирующих звеньев в соответствии с формулами (10.11) и (10.12).

Пассивные дифференцирующ,ие звенья подавляют низкие частоты и вносят положительный фазовый сдвиг. Подавление низких частот обычно недопустимо, так как снижает результирующий общхт коэффициент усилешШ и увеличивает ошибки системы регулирования. Если восстановить на низких частотах прежний коэффициент усиления введением дополнительного усиления крт = Go, то передаточная функция звена совместно с дополнительным усилителем будет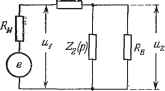

Wip):

,-1 i + TjP

i+TiP

(10.13)

Рис. 10.3. ~ -2P i + TP

Такое звено обладает свойством усиливать высокие частоты в Т/Т раз. Асимптотическая л. а. х. этого звена может быть получена из л. а. х., изображенной в табл. 10.1, поднятием ее параллельно самой себе до Совпадения левой горизонтальной асимптоты с осью абсцисс. Л. ф. X. остается без изменений

Пассивные интегрируюиие звенья подавляют усиление на высоких частотах и вносят в некотором интервале частот отрицательный фазовый сдвот.

Интегро-дифференцирующие звенья подавляют усиление в некотором интервале средних частот, а вносимый фазовый сдвиг вначале отрицателен, затем с ростом частоты становится нулевым на частоте с = (12) ° = = {ТзТ)~°. При- дальнейшем росте частоты фазовый сдвиг становится положительным. Подавление усиления в области средних частот происходит в соответствии с относительным значением модуля РГпз (/ ) на средней частоте:

(1-Ь/ЮсГ1)(1-}-/ЮсГ2)

(1-(-/ШсГз)(1 + /Мс74)

У1+У2

(10.14)

Фазосдвигающ,ие звенья вносят отрицательный фазовый сдвиг при равенстве единице модуля частотной передаточной функции, \ Wa {1) I = I1 что соответствует прохождению гармонического сигнала любой частоты без изменения его амплитуды.

Таблица 10.1

Название п схема пассивного звена

Передаточная функция

Частотные характеристики

Параметры

Л. а. x. и л. ф. x.

Дифференцирующее

Vl + cori 1р = arctg wi - arctg tofg

Ri+R R1+R2

Lo = 201gGo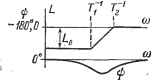

Дифференцирующее С,

1+Г1Р

Vl + tori г); = arctg (oTi - arctg ыТ

Ti = RiCi;

2 = 5-IP I p 1>

Л + До + Л1

0 .

Gcx,=

Ri,+Ro

io = 201gGo; boc = 201gGoo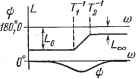

Интегрирующее

1 + Г2Р 1 + Г1Р

У1+юг .

Vl+cdr

ф = arctg сйгг - arctg сйг)

1 + 2)2;

2 = 22! 2 2

Gcx,=

R1 + R2 Ti Z,oo = 201gGoo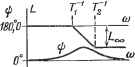