ГЛАВА 10

УЛУЧШЕНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ § ЮЛ. о корректирующих средствах

Под улучшением качества процесса регулирования, помимо повышения точности в типовых режимах, понхшается изменение динамических свойств системы регулирования с целью получения необходимого запаса устойчхшо-сти и быстродействия. В этой проблеме основное значение имеет обеспечение запаса устойчивости. Это объясняется тем, что стремление снизить ошибки системы регулирования приводит, как правило, к необходимости использовать такие значения общего коэффициента усиления, при которых без принятия специальных мер система вообще оказывается неустойчивой.

При решении задачи повышения запаса устойчивости проектируемой системы регулирования прежде всего необходимо попытаться рациональным образом изменить ее параметры (коэффициенты передачи отделышх звеньев, постоянные времени и т. п.) так, чтобы удовлетворить требованиям качества регулирования, которые определяются критериями качества. При невозможности решить эту задачу в рамках имеющейся системы приходится идти на изменение ее структуры. Для этой цели обычно используется введение в систему регулирования так называемых корректирующих средств, которые должны изменить динамику всей системы в нужном направлении. К корректирующим средствам относятся, в частности, корректирующие звенья, представляющие собой динамические звенья с определенными передаточными функциями.

В тех случаях, когда корректирующие звенья используются именно для получения устойчивости системы регулирования или для повышения ее запаса устойчивости, они называются иногда демпфирующими или стабили-зирующхши звеньями. При этом имеется в виду, что звенья демпфируют колебания, которые возникают в системе регулирования. Термин корректирующие звенья является более широким и используется для звеньев, которые вводятся в систему для изменения статических и динамических свойств с различными целями.

Получение требуемого быстродействия обычно обеспечивается при проектировании системы регулирования посредством выбора соответствующих элементов цепи регулирования (исполнительных органов, усилителей, серводвигателей и т. п.). Однако возможно улучшение быстродействия системы посредством использования корректирующих средств.

Замет1Ш также, что проблема получения в системе регулирования требуемых качественных показателей - точности в типовых режимах, запаса устойчивости и быстродействия - является единой и ни один из входящих в нее вопросов не может решаться в отрыве от других. Это делает всю проблему весьма слончной, что заставляет в некоторых случаях получать требуемое решение посредством последовательного приближения и рассмотрения многих вариантов.

Корректирующие звенья могут вводиться в систему регулирования различными способами.

На рис. 10.1, а представлена схема введения в цепь регулирования корректирующего устройства последовательного типа. Здесь Wc {р) представляет собой передаточную функцию части цепи регулирования, W- {р) - передаточную функцию последовательного корректирующего звена.

Результирующая передаточная функция может бьггь найдена из выражения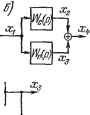

(10.1)

На рис. 10.1, б представлена схема введения в цепь регулировашш коррек- Рис. 10.1.

тирующего устройства параллельного

типа, имеющего передаточную функцию W (р). Результирующая передаточная функция

( =-3-=-7+-г = ()+и(р).

(10.2)

На рис. 10.1, в изображено корректирующее устройство, выполненное в виде местной обратной связи. Результирующая передаточная функция находится следующим образом.

На вход звена с передаточной функцией W, (р) поступает сигнал х, равный сумме или разности входного сигнала х и сигнала х, поступающего по цепи обратной связи:

Х Xi -f- х.

Знак плюс соответствует положительной обратной связи, а знак минус-отрицательной обратной связи.

Сигнал обратной связи х = Woe ip) s-В результате получим

3 = Wo (р) х = Wc {р) [xi ± Woe ip) ж3]

3 [1 + Wo (р) Woe iP) = Wo {p} Xi. Отсюда можно найти результирующую передаточную функцию:

Wo (Р)

(10.3)

Wo (Р) Woe (Р)

В этом выражении знак минус соответствует положительной обратной связи, а знак плюс - отрицательной.

В качестве корректирующих устройств обычно применяют отрицательные обратные связи, хотя не исключена возможность использования и положительных обратных связей. Поэтому в дальнейщем будем использовать формулу (10.3) со знаком плюс, считая, что она записана для отрицательной обратной связи:

Wo(P)

Woip).

(10.3)

1 + Ис(р)Иос(Р)

Использование того или иного типа корректирующих устройств, т. е. последовательных звеньев, параллельных звеньев или обратных связей, определяется удобством технического осуществления.

В линейных системах динамические свойства их при введении корректирующих устройств различного типа могут быть сделаны одинаковыми, и для корректирующего устройства одного типа можно подобрать эквивалентное корректирующее устройство другого типа. Эквивалентность означает, что присоединение к системе регулирования одного или другого корректирующего устройства образует полностью подобные в динамическом отношении системы.

Для получения формул перехода от корректирующего устройства одного типа к корректирующему устройству другого типа необходимо приравнять результирующие передаточные функции (10.1) - (10.3). В результате имеем

(р) РГ з ip) = ip) 4- ip) = ity;)t(p) . (10.4)

Отсюда можно получить шесть формул перехода от передаточной функции звена одного типа к передаточной функции звена другого типа:

(р)-щ§Г (10.7)

ip) = We (р) [ Wns {Р) ~ 1], (10.8)

Звенья последовательного типа особенно удобно применять в тех случаях, когда в системе регулирования используется электрический сигнал в виде напряжения постоянного тока, величина которого функционально связана с сигналом ошибки и = / (ж), например, линейной зависимостью и = кх. Тогда корректирующее звено может быть осуществлено При помощи R-, С- и L-элементов.

Эти звенья оказываются значительно менее удобными, если сигнал представляет собой модулированное напряжение переменного тока. В этом случае имеется принципиальная возможность построения звеньев на тех же R-, С-и L-элементах, воздействующих на огибающую модулированного сигнала, но ввиду их сложности и недостатков они пока почти не находят применения. При наличии модулированного сигнала и при необходимости использовашш звеньев последовательного типа приходится устанавливать в канале переменного тока фазочувствительный демодулятор. После выпрямления и фхшь-трации сигнала от высших гармоник в этом случае появляется возможность ввести звено последовательного типа. Схема введения звена последовательного типа изображена для этого случая на рис. 10.2. Модулированный сет-нал переменного тока поступает на фазочувствителымй демодулятор ФД, затем после выпрямления на фильтр Ф и далее на последовательное корректирующее звено ИЗ. В случае необходимости вести дальнейшее усиление на переменном токе после последовательного звена устанавливается модулятор М. Однако такой путь часто связан с серьезным ухудшением динамических свойств системы вследствие влияния дополнительных постоянных времени фильтра, устанавливаемого на выходе демодулятора.

Звенья параллельного типа удобно применять в тех случаях, когда необходимо осуществить сложный закон регулирования с введением интегра-