§ 9.3. Неединичные обратные связи

Неединичные обратные связи применяются для уменьшения ошибки, вызванной задающим воздействием в замкнутой системе регулирования.

Рассмотрим структурную схему, изображенную на рис. 9.15. В отличие от обычной схемы регулируемая величина у {£) поступает на сравнение в чувствительный элемент по главной обратной связи с передаточной функцией, не равной единице, i. е. -ip {р) ф1.

В этом случае регулируемая величина в функции задающего воздействия будет определяться выражением

(9.54)

Для получения полной инвариантности необходимо выполнить условие Фэ {р) = 1- Отсюда можно найти требуемую передаточную функцию главной обратной связи:

При разложении этого выражения в степенной ряд получаем * ip) = о - (TiP + тр -f xIp +...).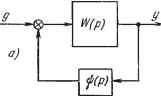

(9.56)

Отсюда видно, что для получения полной инвариантности необходимо использовать главную обратную связь с коэффициентом передачи, в общем случае отличным от единицы: а ф\ (в астатических системах а = i), и дополнительно ввести положительные обратные связи по производным от регулируемой величины.

Реализация полной инвариантности, т. е. реализация условия (9.55), практически невозможна. Это определяется, во-первых, невозможностью точного введения высших производных (9.56), а во-вторых, тем, что при выполнении условия (9.55) система будет находиться на границе устойчивости. Поэтому неединичные обратные связи используются лишь как средство повышения точности замкнутой системы регулирования.

Аналогично тому, как это делалось для систем комбинированного управления, структурную схему с неединичной обратной связью (рис. 9.15, а) можно заменить эквивалентной схемой с единичной главной обратной связью, но с некоторой эквивалентной передаточной функцией разомкнутой системы (р)- Последняя может быть определена из равенства передаточных функций замкнутой системы двух схем (рис. 9.15, а и 9.15, б):

Рис. е.15.

Отсюда находим

W,{p) =

Wjp)

{p)]W(p)

(9.57)

(9.58)

Наиболее эффективным действие неединичной обратной связи оказывается в статической системе. Здесь простым изменением коэффициента передачи жесткой главной обратной связи можно получить астатизм относительно задающего воздействия.

W{p) =

Для ТОГО чтобы показать это, рассмотрим передаточную функцию разомкнутой статической системы (5.36):

i + Cn-iP+.-. + Cop-

Будем считать, что главная обратная связь жесткая, т. е. ij; (р) = а. Тогда эквивалентная передаточная функция разомкнутой системы (9.58) будет

И- К{1 + Вп,1р+...-\-Ворш)

ЛР)~- (1 + с ,р+.--+СоР )-(1- о)ЛГ(1+£, ,р+...+ВоР ) Нетрудно видеть, что при выполнении условия

(1-ао)/Г = 1

(9.59)

(9.60)

K-i , 1

с = -- = 1 -

(9.61)

в знаменателе (9.59) пропадает член с оператором в нулевой степени. В этом случае эквивалентная передаточная функция разомкнутой системы будет соответствовать астатизму первого порядка:

K{l+Brr, iP+...+Bopr)

Эта система будет обладать добротностью по скорости

(9.62)

(9.63)

Taihm образом, при помощи совершенно элементарного приема - уменьшения коэффициента передачи главной обратной связи на незначительную

l i

i---1

Рис. 9.16.

величину по сравнению с единицей - можно получить в системе астатизм первого порядка относительно задающего воздействия, что будет означать отсутствие статической ошибки и равенство нулю первого коэффициента ошибки: Со = 0.

Следует заметить, что аналогичные результаты, т. е. уничтожение статической ошибки от задающего воздействия в статической системе, можно получить не менее простьш способом масштабирования входной или выходной величины системы регулирования (рис. 9.16).

Если на входе или выходе системы включить масштабирующее устройство с коэффициентом передачи

Я-f 1

то регулируемая величина у (t) будет связана с задающим воздействием g (t) соотношением

W(p) K+l

yit)

l+W К

git)-

(9.64)

В установившемся режиме при статическом регулировании W (0) = К. Поэтому для установившегося режима при g {t) = = const

YCT go = go. (9.65)

что соответствует отсутствию статической ошибки. Такое масштабирование делается практически во всех статических системах регулирования, что позволяет рассматривать их по отношению к задаюп],ему воздействию как астатические и считать для них коэффициент ошибки Cq = 0.

Однако равенство нулю первого коэффициента ошибки в статических системах может быть достигнуто при выполнении. условия К = const, что следует из приведенных вьппе формул. Если обилий коэффициент усиления нестабилен, то нетрудно показать, что в системе появится статическая ошибка

Жует = 7 (9.66)

где - относительное изменение коэффициента усиления по сравнению с расчетным значением. Следовательно, первый коэффициент ошибки в этом случае будет равен Сд