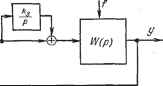Рис. 9.7.

W(p)

Рис. 9.8.

например, астатизм первого порядка, то система рис. 9.7 с изодромными устройствами будет обладать астатизмом четвертого порядка. В этом случае для коэффициентов ошибок будет иметь место равенство = Cj = = = Cg = 0. Как и ранее, при соответствующем выборе постоянных времени

11 1

изодромных устройств = -р-, = -7- и = -т- МОЖНО сохранить

К\ 2 3

практически те же условия устойчивости, что и в исходной системе.

Регулирование по производным от ошибки. В большинстве случаев регулирование по производным от ошибки имеет целью повысить запас

устойчивости системы, что позво-Даффсрещирующииэлеснп, увеличить общий коэффициент

усиления системы и тем самьш улучшить точность регулировашш. Это будет рассмотрено более подробно в главе 10.

Однако регулирование по производным от ошибки может самостоятельно повышать точность системы регулирования даже в том случае, когда сохраняется неиз= менным общий коэффициент усиления в системе. Физика этого явления заключается в том, что при введении регулирования по производ-ньш система начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. В результате система регулирования более быстро реагирует на появление задающих и возмущающих воздействий, что снижает ошибку регулирования.

Структурная схема введения производной по ошибке изображена на рис. 9.8. Передаточная функция части прямого канала вместе с включенным дифференцируюпщм элементом может быть представлена приближенно (в предположении, что дифференцирующий элемент является идеальным) в виде

Р7д(р) = 1 + Гдр, (9.21)

где - постоянная времени дифференцирующей цепи.

В качестве дифференцирующих элементов могут, например, применяться устройства, изображенные на рис. 4.23 и 4.24.

Рассмотрим в качестве примера ту же следящую систему (рис. 6.4). При введении производной от ошибки при помощи тахогенераторов, установленных на командной и исполнительной осях, электромеханическая схема

Для дальнейшего повышения порядка астатизма системы регулирования могут применяться не один, а два, три и т. д. изодромных устройства. В этом случае можно получить повышение порядка астатизма на один, два, три ИТ. д. в зависимости от необходимости. На рис. 9.7 в качестве примера приведена структурная схема системы с тремя изодромными устройствами, т. е. схема с тройным изодромированием. Если исходная система имеет.

будет иметь вид, изображенный на рис. 9.9. Здесь приняты следующие обозначения: СКВТ - синусно-косинусные вращающиеся трансформаторы, ТГ - тахогенераторы, Д - двигатель, Р - редуктор.

Передаточная функция разомкнутой системы может быть получена умножением (9.1) на передаточную функцию (9.21). В результате получим

W( . К(1 + ГдР)

(9.22)

где постоянная

Гд представляет собой отношение передаточного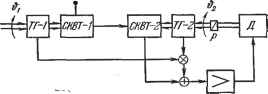

Рис. 9.9.

коэффициента тахогенератора/к передаточному коэффициенту чувствительного элемента (СКВТ), т. е.

Для передаточной функции разомкнутой системы (9.22) находим пере-

даточную функцию по ошибке:

1 р{+ТурШ-\гТр)

р (1 -Ь Тур) (1 -ь г р) -Ь я (1 -Ь Трр)

(9.23)

\ + W{p)

Раскладывая ее в ряд, получаем соотношения для коэффициентов ошибок:

1,(9.24)

Сравнивая последние выражения с (9.2), можно заметить, что коэффициенты Сг и Cg (а также следующие коэффициенты) уменьшаются при введении регулирования по первой производной от ошибки. При соответствующем выборе величины постоянной времени Гд можно добиться условий Cg = О или Сз = 0. При Cg = О система не будет иметь установившейся ошибки, пропорциональной ускорению.

Аналогичным образом, применяя два включенных последовательно дифференцирующих элемента, можно получить равенство нулю одновременно двух коэффициентов, например Cg = О и Сд = 0. В этом случае можно показать, что в системе, наряду с регулированием по первой производной от ошибки, будет использоваться регулирование по второй производной. Это вытекает из того, что передаточная функция двух дифференцирующих

252 ПОВЫШЕНИЕ;;ТОЧНости СИСТЕМ1.АВТ0МАТИЧЕСК0Г0 РЕГУЛИРОВАНИЯ [ГЛ.

элементов, включенных друг за другом в соответствииJc рис. 9.8, будет равна произведению двух передаточных функций типа (9.21):

Ип (Р) = (1 + TiP) (1 +W = 1 +iP+ тр, (9.25)

где Tj = + Гдз представляет собой отношение коэффициентов передачи по первой производной и по ошибке, а т = Гд1Гд2 - отношение коэффициентов передачи по второй производной и по ошибке.

Как видно из рассмотренного, в отличие от случая введения изодромного устройства (см. рис. 9.4), когда обращается в нуль первый, ранее отличный от нуля коэффициент ошибки, введение дифференцирующего элемента (рис. 9.8) не влияет на этот коэффициент ошибки, но зато уменьшает последующие коэффициенты. В связи с этим наиболее эффективное снижение ошибки системы регулирования может быть достигнуто при одновременном использовании изодромных устройств и дифференцирующих элементов.

Так как дифференцирование эквивалентно дополнительному усилению верхних частот, то использование более чем двух дифференцирующих элементов оказывается затруднительным вследствие возрастания влияния высокочастотных помех. Число же изодромных устройств ограничивается только получающимся усложнением системы регулирования. Однако и оно обычно не превьппает трех.

§ 9.2. Теория инвариантности и комбинированное управление

Одним из способов, позволяющих получить высокую точность в системах автоматического регулирования, является использование методов так называемой теории инвариантности [74, 129]. Система автоматического регулирования является инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, регулируемая величина и ошибка системы не зависят от этого воздействия. Система автоматического регулирования является инвариантной по отношению к задающему воздействию, если после завершения переходного процесса, определяемого начальнььми условиями, ошибка системы не зависит от этого воздействия.

Оба этих понятия имеют общую математическую трактовку. Рассмотрим эту трактовку для случая, когда на систему действует одно входное воздействие - задающее g (t) или возмущающее / (t). Пусть для ошибки системы регулирования имеет место дифференциальное уравнение

(аоР + aip - -{-...+an) X it) = (Ьор + bip + ...+b)i (f),

(9.26)

где ij5 (t) - задающее или возмущающее воздействие, а р = ~ ,

Решение этого уравнения имеет две составляющие - переходную Жп (О и вынужденную Жв(). Переходная составляющая определяется общим решением уравнения (9.26) без правой части, а вынужденная - частным решением уравнения (9,26) с правой частью.

Изображение ошибки х (t) при нулевых начальных условиях можно представить в следующем виде:

Q (р) = ЬоР + bip- -ь ... + ь,

D {р)!-~ оор -Ь а,р - -f . . . -Ь а .