Логарифмические характеристики для передаточной функции (9.3) построены на рис. 9.3 по выражениям:

L(co)201g (9.8)

я]; (со) = - 180° - arctg соГу - arctg аТ

(9.9)

Сравнение рис. 9.3, а и 9.3, б, а также формул (9.7) и (9.9) показывает, что введение интегрирующего элемента дает дополнительный фазовый сдвиг (-90°), в результате чего в рассматриваемой схеме нельзя добиться устойчивой работы ни при каком значении общего коэффициента усиления. Однако это не означает, что схема является вообще неработоспособной.

Ивсдромный элемент

Рис. 9.4.

Введение в нее корректирующих средств (см. главу 10) позволяет не только достичь устойчивости, но и обеспечить определенный запас устойчивости, т. е. выполнить требования к качеству процесса регулирования.

Применение йзодромных устройств. Существует путь повышения порядка астатизма системы регулирования без заметного или недопустимого ухудшения ее запаса устойчивости. Этот путь заключается в применении йзодромных устройств, например таких, как изображенные на рис. 4.22. Структурная схема системы регулирования при введении изо дромного устройства изображена на рис. 9.4. Передаточная функция изодромного устройства может быть представлена в виде

(р) = 1

(9.10)

тде Ги = -;--постоянная времени изодромного устройства.

Пример введения изодромного устройства показан на рис. 9.5. На рис. 9.5, а изображен чувствительный элемент регулятора давления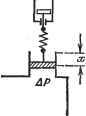

,

Рис. 9.5.

С противодействующей пружиной. Если не учитывать массу движущихся частей, то перемещение чувствительного элемента будет пропорциональным -отклонению давления от заданного значения:

X = fciAP, (9.11)

тде &1 -коэффициент пропорциональности, определяемый жесткостью пружины.

На рис. 9.5, б изображен тот же элемент, но с противодействуюш;им демпфером. Так как сила, развиваемая демпфером, пропорциональна скорости перемеш;ения его поршня, то в этом случае будет иметь место соотношение рх = кАР. Вместо (5.11) получим

x = hP, (9.12)

где 2 - коэффициент, определяемый скоростным сопротивлением демпфера.

Равенство (9.12) соответствует введению интеграла в закон регулирования.

Наконец, в случае, изображенном на рис. 9.5, в, перемещение чувствительного элемента будет складываться из деформации пружины и перемещения поршня демпфера:

=(/сД)др = А(1±ад.др, (9.13)

где = - постоянная времени изодромного устройства.

В качестве второго примера рассмотрим приведенную выше схему следящей системы (рис. 9.2). Переход от введения дополнительного интеграла к введению изодромного устройства может быть сделан добавлением связи, показанной пунктиром. Передаточная функция разомкнутой системы может быть получена умножением (9.1) на передаточную функцию изодромного устройства.

В результате для рассматриваемой схемы получим:

W(r>\ и(1 + ад в(1 + ГиР) /ош

S \Р) р(1 + Гур)(1-1-ЗД р P(i + Typ){i + Tp) * >

где Кг = KiK [ПсекЦ - добротность системы по ускорению. Коэффициенты ошибки определяются равенствами:

со = с, = 0, if=-, Jil±If=Ij.y (9.15)

Рассматривая; характеристическое уравнение системы

\TyTp + (Ту + TJ р+Р + К,Т р -f = О,

можно убедиться, что в системе возможно получение устойчивости при выполнении условия

или,в ином!вЕде,

Нетрудно видеть, что при Уи °° (это будет при отсутствии интегрирующего привода в изодромном механизме) условие устойчивости переходит в неравенство

К<:+-, (9.18)

у) м

которое скраведливо для исходной схемы, изображенной на рис. 6.4. При достаточно больших значениях постоянной времени изодромного механизма Ги, что соответствует малому передаточному коэффициенту интегрирующего

привода fe = , условия устойчивости (9.16) и (9.17) будут мало отли-

и

чаться от условия устойчивости (9.18) исходной схемы. Таким . образом, введение изодромного механизма с относительно большой постоянной времени дает повышение порядка астатизма на единицу при возможности практически сохранить условия устойчивости в системе, куда этот механизм вводится.

Это обстоятельство можно проиллюстрировать также на логарифмических частотных характеристиках (рис. 9.6). В соответствии с выражением для передаточной функции разомкнутой системы (9.14) можно записать:

-т,о- -

-90°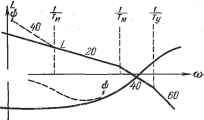

Рис. 9.6.

L(co) = 20 Ig

£0

(9.19)

х\ (со) = (-90° - arctg соГу - arctg соГм) - 90° + arctg соГи- (9.20)

Сравнивая эти выражения с формулами (9.6) и (9.7) справедливьши для исходной схемы, можно заметить, что при относительно большом значении постоянной времени логарифмические характеристики системы с изодромным устройством будут иметь отличие только в низкочастотной

области при со <: -5;- . Для частот со > дополнительный множитель

в (9.19) обращается в единицу, а дополнительный фазовый сдвиг в (9.20) равен нулю. Таким образом, при со >логарифмические частотные характери-

и

стики системы с изодромным устройством практически не отличаются от логарифмических характеристик исходной схемы. В частности, в районе нуля децибел для п. а. х. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одинаковому запасу устойчивости.

На рис. 9.6 сплошными линиями показаны л. а. х. и л. ф. х. для исходной схемы, а пунктирными - изменения, даваемые введениемизодромного устройства с относительно большой постоянной времени.

Следует заметить, что введение изодромного устройства с большой постоянной времени образует систему, динамические качества которой могут оказаться сравнительно низкими. Это объясняется тем, что введение такого устройства улучшает вид амплитудной характеристики только в низкочастотной области (рис. 9.6). В результате коэффициенты ошибки, следующие за тем коэффициентом, который обращается в нуль, могут не только не уменьшиться, но даже возрасти.

В рассмотренном выше примере при введении изодромного устройства обратился в нуль коэффициент Cj (9.15). Однако в следующие коэффициенты

в качестве делителя входит добротность по ускорению = -тр- При боль-

шом значении постоянной времени добротность системы по ускорению Ке получается малой и коэффициенты ошибок

2 з? СИЛЬНО возрйстают,-