/ЛАВА 9

ПОВЫШЕНИЕ? ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 9.1. Общие методы

К числу общих методов повышения точности систем автоматического регулирования относятся:

1) увеличение коэффициента усиления разомкнутой цепи;

2) повышение степени астатизма;

3) применение регулирования по производным от ошибки. Увеличение общего коэффициента усиления разомкнутой цепи является

наиболее универсальным и эффективным методом. Увеличить общий коэффициент усиления можно обьино за счет введения в систему регулирования усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.

Увеличение общего коэффициента усиления благоприятно сказывается в смысле уменьшения ошибок практически во всех типовых режимах. Это вытекает, в частности, из того, что общий коэффициент усиления разомкнутой цепи входит в качестве делителя во все коэффициенты ошибок (см. пример, рассмотренный в § 8.3).

Однако увеличение общего коэффициента усиления ограничивается устойчивостью системы регулирования. При повьыпении коэффициента усиления, как правило, система приближается к колебательной границе устойчивости. При некотором предельном его значении в системе возникают незатухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы регулирования.

В связи с этим повышение общего коэффициента усиления до значения, при котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повьппении запаса устойчивости системы, что осуществляется при помощи так называемых корректирующих средств, рассматриваемых в следующей главе.

Повышение порядка астатизма. Повышение порядка астатизма используется для устранения установившихся ошибок в различных типовых режимах: в неподвижном положении, при движении с постоянной скоростью, при движении с постоянным ускорением и т. д. Формально это сводится к тому, чтобы сделать равными нулю первые коэффициенты ошибки системы, например, Ср = О при астатизме первого порядка, или Ср = = О при астатизме второго порядка, или Cq = = = О при астатизме третьего порядка и т. д. Физически повышение порядка астатизма осуществляется за счет введения в канал регулирования интегрирующих звеньев. В качестве таких звеньев могут, например, использоваться звенья, изображенные на рис. 4.21. Структурная схема системы регулирования с введенным шиге-

грирующим звеном изображена на рис. 9.1. Передаточная функция интегрирующего звена

где к -1 - коэффициент передачи интегрирующего звена. W (р) пред-

1 С€К

ставляет собой передаточную функцию разомкнутой системы регулирования до введения интегрирующего звена.

Результирующая передаточная функция разомкнутой системы будет иметь дополнительный множитель р в знаменателе:

knW{p)

Повышение порядка астатизма неблагоприятно сказывается на устойчивости системы. Поэтому одновременно с повышением порядка астатизма в системе автоматического регулирования приходится использовать корректирующие звенья, повышаюпще

запас устойчивости (см. главу 10).

В качестве иллюстрирующего примера рассмотрим систему, изображенную на рис. 6.4. Для нее была получена передаточная функция разомкнутой системы в виде

W(p)

Рис. 9.1.

которая соответствует астатизму первого порядка.

В соответствии с примером, рассмотренным в § 8.3, первые коэффициенты ошибки можно записать следующим образом (если положить - Tl,

= т к=- ку.

(9.2)

Введем в систему интегрирующее звено, например интегрирующий привод. Соответствующая этому случаю электромеханическая схема изображена на рис. 9.2. В этой схеме приняты следующие условные обозначения: СКВТ - синусно-косинусные вращающиеся трансформаторы, ЛЕТ - линейный вращающийся трансформатор, Д - двигатели, Р - редукторы, ТГ - тахогенератор. Передаточная функция исходной системы без интегрирующего звена (9.1) была выведена в § 6.2. Передаточная функция разомкнутой системы, изображенной на рис. 9.2, будет отличаться от (9.1) наличием дополнительного множителя kjp, который дает интегрирующее звено. В результате получим передаточную функцию разомкнутой системы в виде

где Кг = к К

p{i + TyP){i + Tp) Р P{i + Typ){i + Tp) - добротность системы по ускорению.

P4i+Typ){i+Tp)+K

(9.4)

Раскладывая эту функцию в ряд делением числителя на знаменатель, получаем вместо (9.2) следующие равенства для коэффициентов ошибок:

Co = ci = 0,

(9.5)

Для изоврошоео устройстве

тг =0: м1гг

Сравнивая (9.5) с (9.2), можно заметить, что в результате введения интегрирующего звена вследствие повышения порядка астатизма получено условие Ci = О, и, следова-

\ тельно, будет равна нулю

скоростная составляющая

ошибки.

Однако, если проверить теперь систему на устойчивость, можно убедиться, что система вообще не может работать, так как получить устойчивую работу нельзя ни при каком значении общего коэффициента усиления К,. Это называется структурной неустойчивостью. Действительно, передаточной функции (9.3) соответствует характеристическое уравнение

ТуТр + (Ту + TJ + р + = О,

в котором отсутствует член, содержащий оператор в первой степени. Пропуск одного из членов в характеристическом уравнении всегда соответствует неустойчивости в соответствии с § 6.1.

Рис. 9.2.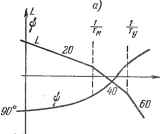

-т,р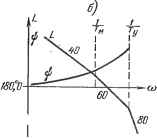

~до-

Рис. 9.3.

Появление неустойчивости в рассматриваемой системе при повьппении порядка астатизма можно проиллюстрировать на логарифмических характеристиках. Логарифмические характеристики для передаточной функции (9.1) построены на рис. 9.3 по выражениям:

L(cu) = 201g--jrz

ф = 90° - arctg соГу - arctg соГм.

(9.6) (9.7)

Эта передаточная функция соответствует уже астатизму второго порядка. Передаточная функция системы по ошибке