Если ири проектировании системы ставится условия, чтобы ее показатель колебательности был не больше некоторого заданного значения, например Afmax = 1.5, то для выполнения этого необходимо, чтобы амплитудно-фазовая характеристика не заходила внутрь окружности, соответствующей этому значению М (рис. 8.27). Амплитудно-фазовая характеристика может только коснуться этой окружности. В этом случае показатель колебательности будет как раз равен заданному значению Мщах-

Таким образом, окружность Tlf щах является запретной зоной для амплитудно-фазовой характеристики разомкнутой системы. Эта зона охватывает точку (-1, /0) и обеспечивает получение заданного запаса устойчивости.

Величина показателя колебательности может быть определена и в случае использования логарифмических частотных характеристик. Для этого отобразим запретную зону (рис. 8.27) на логарифмическую сетку. Рассмотрим отдельно окружность заданного показателя колебательности (рис. 8.28).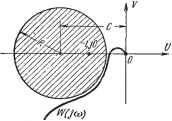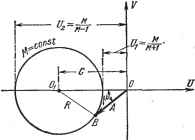

Рис. 8.27.

Рис. -8.28.

На окружности возьмем произвольную точку В и построим вектор, соединяющий эту точку с началом координат. Установим для этого вектора связь между его модулем А и запасом по фазе \i. Из треугольника ОВО по теореме косинусов находим

cofx = -

Далее можно найти

ш окончательно

р. = arccos

(8.86)

Из, рис. 8.28 нетрудно видеть, что зависимость (8.86) существует только для модулей, лежащих в пределах

(8.87)

<А<

В] случае, когда А < jjf или А >fj-t запас по фазе может

быть любым, так как в этом случае конец вектора не может попасть в запретную зону (рис. 8.28).

Задаваясь различными значениями показателя М = const, а следовательно и С = const (8.84), по выражению (8.86) можно построить графики (X = / (А), которые носят название [х-криеых. Эти графики строятся обычно таким образом, что модуль А откладывается в децибелах (рис. 8.29).

Из выражения (8.86) можно найти, в частности, максимальный запас по фазе обычным методом отыскания максимума:

Ишах = arccos

=arccos-

(8.88)

Этот максимум получается, когда модуль А=УС. Если имеется построенная л. а. X. (рис. 8.30), то по имеющимся р-кривым и при заданном значении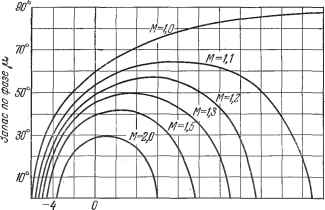

4 8/2 Модуль в децибелах

Рис. 8.29.

М можно построить требуемое значение запаса по фазе для каждого значения модуля. Это построение должно делаться для модулей, лежащих в пределах (8.87). В результате будет gg I получена запретная область для

, фазовой характеристики. Чтобы

т показатель колебательности был

не больше заданного значения, фазовая характеристика не должна заходить в эту область. Нетрудно видеть, что определение качественного показателя, характеризующего запас устойчивости, делается здесь одновременно с определением устойчивости.

Удобство показателя колебательности определяется также тем, что запас устойчивости характеризуется здесь одним числом, имеющим для достаточно сравнительно узкие пределы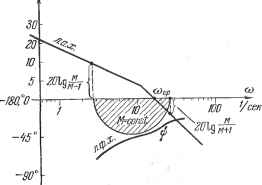

Рис. 8.30.

широкого класса систем регулирования (1,1-1.5).

Оценка быстродействия может производиться по частотным характеристикам замкнутой и разомкнутой системы. При рассмотрении замкнутой системы обычно используется амплитудная частотная характеристика (рис. 8.25) или вещественная характеристика (рис. 8.6). Использование вещественной характеристики было рассмотрено выше (см. § 8.5).

Для оценки быстродействия но амплитудной частотной характеристике (рис. 8.25) могут использоваться следующие величины:

сор - резонансная частота, соответствующая пику а. ч. х.;

СОп - частота, соответствующая полосе пропускания замкнутой системы и определяемая из условия А {(Hj) = 0,707;

СОс - частота среза, соответствующая условию А (cuJ = 1;

cOg - эквивалентная полоса пропускания замкнутой системы, определяемая по выражению

С0з= j Ф(7со) pdco, - (8.89)

где I Ф (/со) I = А (со).

Эквивалентная полоса пропускания представляет собой основание прямоугольника (рис. 8.25), высота которого равна единице, а площадь равна площади под кривой квадратов модуля Ф (/со). Понятие эквивалентной полосы пропускания тесно связано с вопросом пропускания системой помех, что будет рассмотрено в главе 11.

В отличие от показателя колебательности, который является некоторой безразмерной характеристикой и лежит в сравнительно узких пределах, приведенные выше характерные частоты, определяющие быстродействие системы, имеют размерность и их допустимые значения могут сильно меняться в зависимости от типа и назначения системы регулирования. Здесь наблюдается полная аналогия с критериями качества, основанными на рассмотрении кривых переходного процесса. Допустимое значение перерегулирования о% (рис. 8.3) лежит в сравнительно узких пределах для систем самого различного назначения, а допустимое время переходного процесса может меняться от долей секунды до нескольких часов и более.

Допустимые для данной системы регулирования значения сОр, сОп, со с или соэ должны устанавливаться для каждой конкретной системы на основе изучения условий ее эксплуатации. При этом характеризовать быстродействие системы может как вся совокупность указанных выше величин, так и каждая из них в отдельности.

При определении быстродействия по частотной передаточной функции W (/со) разомкнутой системы может использоваться частота среза сорр, которая определяется из условия равенства модуля единице mod W (jcv) = или L (соср) = 0. Эта частота показана, например, на рис. 8.2 и 8.30.

Определение частоты среза разомкнутой системы может быть сделано на диаграмме, изображенной на рис. 8.26, по точке пересечения а. ф. х. с окружностью единичного радиуса, центр которой расположен в начале координат.

Резонансная частота замкнутой системы сОр близка к частоте колебаний системы в переходном процессе. Значение сОр может быть приближенно определено по точке а. ф. х. (рис. 8.26), которая ближе всего расположена к точке (-1, /0).

Частота среза С0(.р во многих случаях близка к резонансной частоте системы СОр.

Удобной и наглядной мерой быстродействия системы является также частота со к, (рис. 8.2), при которой задающее воздействие вида g = = gmax sin СО отрабатываотся системой с амплитудой ошибки не более хах-

Хотя приведенные выше частотные критерии запаса устойчивости и быстродействия могут рассматриваться независимо от свойств системы регулирования во временной области, представляется полезным провести некоторое приближенное сопоставление частотных и временных характеристик.

Если показатель колебательности Af > 1, то замкнутую систему регулирования можно аппроксимировать колебательным звеном (см. § 4.5). Тогда