производные:

что дает

= 0,

АВ - 2 = 0, (АВ - - Л = О,

откуда находим А = 1, В = 2. Следовательно, минимум квадратичной интегральной оценки = 1,5 имеет место в точке D (рис. 8.23). Эта точка лежит, однако, слишком близко к границе устойчивости, что может не обеспечить необходимого запаса устойчивости (см., например, рис. 8.18). Практически лучше брать параметры системы не точно в точке D, а несколько правее и выше.

Этот результат имеет смысл, однако, только в тех случаях, когда &о йд, йд остаются постоянными, а выбираемые параметры системы входят только в коэффициенты и й2 уравнения (8.77).

§ 8.9. Частотные критерии качества

Под частотными критериями качества будем понимать такие критерии, которые не рассматривают вида переходного процесса, а базируются на некоторых частотных свойствах системы. Частотные критерии качества особенно удобно применять при использовании частотных методов расчета, так как при этом получается наиболее простое решение задачи.

Рис. 8.24.

Частотные критерии наиболее разработаны в отношении оценки запаса устойчивости. Запас устойчивости можно определять по удалению амплитудно-фазовой характеристики разомкнутой системы (рис. 8.24, й) от точки (-1, /0). Для этой цели вводятся понятия запаса устойчивости по амплитуде {модулю) и запаса устойчивости по фазе.

Для общего случая условной устойчивости, изображенного на рис. 8.24,й, запас устойчивости по амплитуде определяется двумя точками й и с, и, соответственно, двумя величинами, выраженньши обьгано в децибелах:

Li = 201gpi=201g

L2 = 201gp2 = 201gf/2.

Запас устойчивости по амплитуде тем больше, чем больше и Ь. В хорошо демпфированных системах эти величины составляют примерно 6 -f- 20 дб, что соответствует 2 10 в линейном масштабе.

В случае абсолютной устойчивости смысл имеет только величина Ь, так как оо.

Запасом устойчивости по фазе называется запас по фазе р = 180 -- tj), где tj) - аргумент частотной передаточной функции разомкнутой системы.

соответствующий модулю, равному единице (точка b на рис. 8.24, а):

= 180° + -ф; сдвиг по фазе я]) определяется условием

% = ( ) U(0))=1.

В xoponio демпфированных системах запас по фазе составляет около 30-60°.

В некоторых случаях вместо задания дискретных точек, определяющих запас устойчивости системы регулирования (точки й, и с на рис. 8.24, а),. задают некоторую запретную область для амплитудно-фазовой ха- \Ф(/(о)\ рактеристики разомкнутой системы. Эта запретная область окружает точку (-1, /0) и может быть построена по заданным значениям запаса устойчивости по фазе [х и запаса устойчивости по модулю р (рис. 8.24, б).

Недостатком рассмотренного критерия является то, что для определения запаса устойчивости необходимо задать два числа: р и [х. В этом отношении более удобно

определять запас устойчивости по показателю колебательности. Показателем колебательности называется максимальное значение ординаты Tlfmax амплитудной характеристики замкнутой системы (см. рис. 8.25) при начальной ординате, равной единице, т. е. относительная высота резонансного пика. Физически эта характеристика представляет собой следующее. Если управляющий сигнал на входе системы регулирования меняется по закону g = gmax sin at, то регулируемая величина в режиме установившихся вынужденных колебаний будет меняться по закону у = у шах sin {att -\-+ я)з). Отношение амплитуд Ушнх и g.max определяется модулем частотной передаточной функции замкнутой системы: Ушаж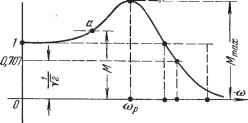

Рис. 8.25.

ё-тах

= mod Ф (/со) = mod . i/?? ч

(8.81)

где W (jai) - частотная передаточная функция разомкнутой системы.

Максимальное значение этого модуля и представляет собой показатель колебательности (имеется в виду наибольший максимум)

Mmax = ©(7C0)Uax=Lx. (8.82)

Как видно из этих рассуждений, показатель колебательности определяется посредством задания задающего воздействия g = gax sin со. В принципе возможно определение показателя колебательности системы посредством задания возмущающего воздействия / = /щах sin со и отыскания относительной величины резонансного пика.

Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Допустимое значение показателя колебательности определяется на основании опыта эксплуатации систем регулирования. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен превосходить значений 1,1 -f- 1,5, хотя в некоторых случаях можно допускать величины до 2 2,5.

Для отыскания показателя колебательности системы регулирования нет необходимости строить амплитудную частотную характеристику (рис. 8.25).

ИЛИ отыскивать максимум (8.82). Сугцествуют приемы, позволяющие найти показатель колебательности по виду амплитудно-фазовой характеристики разомкнутой системы. Возьмем на амплитудной характеристике (рис. 8.25) некоторую точку а, которой соответствует ордината М, и отобразим эту точку на комплексную плоскость частотной передаточной функции разомкнутой системы. Для этого рассмотрим уравнение

mod Ф (/со) =

l-fPF(/(o)

Сделаем подстановки С/ = Ке W (/со) и V - \mW {j(o) Тогда

U+iV\

Возводя в квадрат правую и левую части и освобождаясь от знаменателя, после алгебраических преобразований получим

М2 -1

(8.83)

(8.84) (8.85)

Это есть уравнение окружности с радиусом Дне центром, смещенным влево от начала координат на величину С.

Задаваясь различньвии значениями Af от 1 до со, можно построить емейство таких окружностей (рис. 8.26). На каждой окружности написано

значение ординаты амплитудной частотной характеристики. При М = i окружность вырождается в прямую линию, параллельную оси ординат и проходящую слева от нее на расстоянии 0,5. При М -> оо окружность вырождается в точку, совпадающую с точкой (-1, /0).

Для значений ординат амплитудной характеристики, лежащих в пределах О < Tlf < 1, получается семейство окружностей, расположенных справа от линии М = i, симметрично с первым семейством. При М = О окружность вырождается в точку, совпадающую с началом координат.

Для построения амплитудной характеристики (рис. 8.25) достаточно в тех же координатах, где построены окружности М = const, нанести амплитудно-фазовую характеристику разомкнутой системы. Точки пересечения этой характеристики с окружностями будут определять точки амплитудной характеристики с соответствующими значениями ординат, равными М. Для определения показателя колебательности можно не строить амплитудную характеристику, так как достаточно знать одно максимальное значение ординаты Мщах определяемое по наименьшей окружности М = const, которой коснется амплитудно-фазовая характеристика.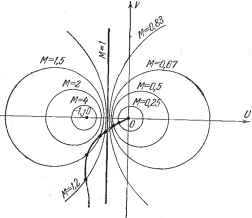

Рис. 8.26.