Методика вычисления интеграла (8.72) сводится к тому, что правая его часть разбивается на два слагаемых:

оо оо

1к= xdt + T\ xdt. о о

При входном воздействии типа единичной ступенчатой функции первое слагаемое последнего выражения соответствует интегральной оценке /, а второе - Т1. Поэтому в результате получаем для этого случая

/к = / + ТЧ. (8.74)

Улучшенная интегральная оценка / может также применяться в безразмерном виде аналогично (8.57) и (8.68):

/ко = /к, (8.75)

где Qo - среднегеометрический корень характеристического уравнения, а С - некоторая величина, имеющая размерность у (t), например статическое отклонение у (оо).

Недостатком приведенных расчетных формул для вычисления как /, так и /к является их выражение через определители, которые трудно бывает раскрывать в буквенном виде при высокой степени характеристического уравнения. В этих случаях можно использовать имеющиеся специальные приемы числовых расчетов. Сам определитель А (8.62), как старший определитель Гурвица, согласно § 6.2 имеет вид

А = Д = 3 ( 12 - о з) - при п = 3,

А = Д = 4 [ 3 (аа, - - аа при п = 4,

А = Д = 5 [( 12 - о з) ( з 4 - 2%) - ( i 4 - 05)1 при п = 5.

Несколько сложнее вычисляется только определитель Д, когда первый столбец А (8.62) с одним элементом Оп заменяется столбцом (8.63) с двумя элементами а и а. Все остальные определители оказываются проще.

Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.

В принципе возможно использование более сложных выражений, чем (8.72), в которые кроме первой производной от отклонения будут входить вторая, третья и т. д. производные. Так, например, ограничившись при подаче ступенчатого воздействия g (t) или / (t) отклонением х, первой производной X и второй производной X, получим интегральную оценку в виде

= J (ж2 + Т\хГ*ж2) dt. (8.76)

Эта оценка будет характеризовать приближение переходного процесса к экстремали, определяемой решением дифференциального уравнения

Tii + Ti x + x = Q.

Экстремаль в данном случае будет соответствовать более сложной кривой, чем экспонента, что позволяет точнее задать желаемый вид переходного процесса. 1

Однако нахождение интегральных оценок вида

/к = / + ПГ + пг,

к которым сводится вычисление интеграла (8.76), сопряжено со значительными трудностями, что ограничивает их применение.

Определение минимума интегральной оценки. Пусть требуется, исходя из минимума какой-нибудь интегральной оценки, выбрать два каких-нибудь параметра аир заданной автоматической системы. Указанные два параметра входят в коэффициенты дифференциального уравнения системы. Прежде всего по вышеприведенным формулам находится выражение соответствующей интегральной оценки. Это выражение, если все параметры системы заданы, кроме аир, имеет вид

/ = /( , Р).

Для определения значений аир, соответствующих минимуму /, вычисляем частные производные по а и р и приравниваем их нулю. В результате получаем два уравнения:

{а, Р) п ЛПа, р) Q da dp

С двумя неизвестными аир. Отсюда и определяются искомые значения параметров аир. Чтобы убедиться в том, что это действительно минимум, а не максимум, можно вычислить значение / при полученных значениях а и р, а затем при каких-нибудь соседних. Последние должны оказаться больше. Аналогично можно поступить и при выборе нескольких параметров по минимуму интегральной оценки.

Функция / (а, Р) не всегда обладает минимумом по рассматриваемым параметрам. Тогда нужно выбирать их по наименьшему значению интегральной оценки / внутри области, назначаемой из других соображений.

Важно также иметь в виду, что выражение интегральной оценки через выбираемые параметры системы в буквенном виде может в ряде случаев оказаться сложным для исследования в общем виде. В таких случаях можно поступить иначе: задавать несколько числовых значений одного из выбирае-1мых параметров (при жестко заданных всех остальных) и вычислять для каждого, из них значения / (или /д). В результате будет видно, при каких значениях данного параметра получается Jmin (можно для наглядности построить график величины / в зависимости от выбираемого параметра). Аналогично нужно поступить и с другими выбираемыми параметрами системы.

В конкретных расчетах всегда надо учитывать, что одновременно с таким выбором параметров нужно, во-первых, обеспечить хорошие статические свойства системы и, во-вторых, проследить, чтобы оптимальная точка не оказалась слишком близкой к границе устойчивости, так как всегда надо иметь некоторый запас устойчивости.

Рассмотрим в качестве примера дифференциальное уравнение третьего порядка

(аер + 12 + ар + а) у (t) = b- (t), (8.77)

где о]; (t) - входное задающее или возмущающее воздействие. Пусть входное воздействие о]; (t) = 1 (t). Тогда изображение по Лапласу регулируемой величины будет

Y(p) = - -

Установившееся значение регулируемой величины здесь будет у {об) =

Вычислим для этого случая интегральную оценку /. Так как п = Ъ, am = О, то в соответствии с формулой (8.61) имеем

Далее по выражению (8.62)] находим определитель

: Us (ctiug-арйз).

Для нахождения До необходимо первый столбец определителя Д заменить на (8.63):

2 -й1 О-

О - йз tti

= 2 (й1а2 - йойд) + йзй.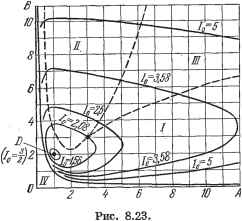

По формуле (8.64) находим единственный коэффициент Bp = Ъ.

В результате получаем значение интегральной квадратичной оценки:

/ = L(f+-?!-).(8.78)

Это выражение и служит для выбора параметров системы, входящих в коэффициенты йо, й, йд, из условия минимума величины /.

Построим диаграмму квадратичной интегральной оценки на плоскости параметров Вышнеградского А ж В. Согласно § 8.7

й1=Ай, й2=Бй.

Подставив этоТвыражение в (8.78), получим

Найдем безразмерную оценку Ip в соответствии с формулой (8.57). Подставляя значение среднегеометрического корня Qp = 1/ - и С = -,

г ар Аз

получаем

(8.79)

При Ip = const это дает на плоскости параметров Вышнеградского кривую

А + {АВ -. 1) (Б -. 21р) = 0. (8.80)

Построенные по этому уравнению кривые постоянных значений оценки Ip нанесены на диаграмме (рис. 8.23). Там же пунктиром нанесены кривые, взятые из диаграммы Вышнеградского (рис. 8.15), показывающие области колебательного (/), монотонного ( ) и апериодического ( /) процессов. Минимум интегральной оценки находим, приравнивая нулю частные