В- -fl--Y

i?n-i-*o Д-ь----} -Ц-ь-){-ъГ /J

R гГ / Ьп-2 ап-2 \ о / t>n-t an-i \ I п-з ге-з

Ъп-i

Ъп-1 = Ьо

(8.66)

При поступлении на вход системы единичного импульса 6 () = 1 {t), изображение которого по Лапласу равно 1, изображение регулируемой величины можно также представить в виде дробно-рациональной функции (8.60). Разница будет заключаться только в том, что степень числителя т возрастает на единицу, а последний коэффициент числителя = 0. Это обусловлено тем, что получение реакции системы на единичный импульс (весовой функции) эквивалентно дифференцированию переходной функции, получающейся при действии единичного скачка. В области изображений это эквивалентно умножению на комплексную величину р.

В связи с этим квадратичную интегральную оценку при действии единичного импульса можно рассматривать в виде выражения

оо оо

(8.67)

где w (t) - весовая функция системы по задающему или возмущающему воздействию, х (t) - отклонение регулируемой величины от нового установившегося состояния в переходном процессе при действии единичной ступеньки задающего или возмущающего воздействия.

Таким образом, техника вычисления оценки / полностью совпадает с вьгаислением оценки / по формуле (8.61) или (8.65). Совпадает при этом и значение определителя А (8.62). Отличаться в вычислениях будут определители Ар, . . А и коэффициенты Вд, . - ., В или В, . . ., Вп, что обусловлено повышением степени т в выражении (8.60) на единицу при вычислении / по сравнению со случаем вычисления /.

Интегральная оценка / также может использоваться в безразмерном виде аналогично формуле (8.57):

Г 0

(8.68)

i Интегральные оценки I ш I (или выражения квадратичных динамических ошибок) применяются для выбора структуры и параметров систем автоматического регулирования. При этом наилучшими параметрами считаются такие, при которых величина / или / имеет минимальное значение.

Вычисление квадратичных интегральных оценок I ж Г можно также производить на основании так называемой формулы Релея, которая будет доказана ниже, в главе 11. Здесь она будет приведена без доказательства.

Если X (/to) есть изображение Фурье функции времени х {t), то существует зависимость, определяемая теоремой Парсеваля (см. ниже стр. 317),

оо +00 оо

xHt)dt = - J Z(/to)pdco=4-JX(7co)pdco,

т. е. интегрирование квадрата функции по времени в пределах от нуля до бесконечности можно заменить интегрированием квадрата модуля изображения Фурье этой функции по всем частотам. При нахождении интегральной оценки /, соответствующей реакции системы на входное задающее воздействие типа 1 (t), изображение Фурье исследуемого отклонения x{t) = у (оо) - - у (t) будет

Х(;со)=Вг. где /со) - частотная передаточная функция замкнутой системы. Тогда

1 = ± Ф(0)-Ф(/.о)Р (8.69)

В астатических системах и статических системах с неединичной обратной связью или с масштабированием (см. § 9.3) установившееся значение у (оо) = = 1 и Ф (0) = 1. Тогда формула (8.69) будет иметь вид

(/со)2

dco.

Г8.70)

где Фж (/со) = 1 - Ф (/со) - частотная передаточная функция замкнутой системы по ошибке.

Аналогичным образом для входного задающего воздействия типа единичного импульса б (t), изображение которого равно 1, изображение Фурье

исследуемого отклонения х (t) = -у (t) равно частотной передаточной функции замкнутой системы: X (/со) = Ф (/ю)-1. В результате получаем

Рис. 8.21.

(8.71)

Подобные выражения могут быть получены и для входного возмущающего воздействия, если вместо частотной передаточной функции Ф (/со) использовать передаточную функцию по возмущающему воздействию Ф- (/со).

Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных по форме процесса, изображенных на рис. 8.21, имеют одно и то же значение квадратичной интегральной оценки (8.56) Часто оказывается, что выбранные по минимуму этой оценки параметры системы соответствуют слишком сильно колебательному процессу, ибо отмечавшееся уже при этом стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установившемуся значению ж = 0.

Это получается вследствие того, что оценка (8.56) учитывает только величину отклонения и быстроту затухания и ншсак не учитывает близость системы к колебательной границе устойчивости.

Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. 8.22, а. Очевидно, что величина интегральной оценки (8.56) будет тем меньше, чем ближе будет кривая переходного процесса к ломаной линии АОБС. Но нри-ближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой 0D к отрезку ОБ).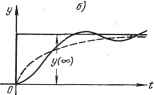

Рис. 8.22.

Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.

Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения ж, но также

и на скорость отклонения х. Эта улучшенная квадратичная интегральная оценка имеет вид

К=\ {x + Tx)dt,

(8.72)

где Т - некоторая постоянная времени.

Выясним, какой вид переходного процесса будет получаться при выборе параметров системы регулирования но минимуму улучшенной интегральной оценки (8.72). Для этого проделаем следующие преобразования:

оо оо оо

/ = J (ж + Тху - J 2Тхх = J (ж + Тху dt - Тх

= J (а: + Tx)dt + Га,

где Хд - начальное значение отклонения в переходном процессе.

Наименьшее значение последнего выражения будет при выполнении

условия тх + X = {Тр + i) X 0.

Это есть дифференциальное уравнение первого порядка, решение которого имеет вид

(8.73)

х = Х(,е

V = yo{i - e ),

где Уо = Хо - установившееся отклонение регулируемой величины.

Этот процесс изображен на рис. 8.22, б пунктиром. Следовательно, выбирая параметры системы по минимуму улучшенной интегральной оценки (8.72), можно приблизить переходный процесс к заданной экспоненте (8.73) с постоянной времени Т, которая носит в этом случае название экстремали. Из этих соображений можно заранее задаться определенной величиной Т.

Выбор параметров системы по улучшенной квадратичной интегральной оценке приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (8.56).