где X {£) - отклонение регулируемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса.

В устойчивой системе ж О при t- оо ж этот интеграл имеет конечную величину. Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. 8.19, а). , е)

Площадь будет тем меньше чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.

Для вычисления интеграла (8.53) нет необходимости в нахождении х (i), так как его можно легко вычислить, используя изображение Лапласа или Хевисайда - Карсона. Действительно, изображение Лапласа определяется выражением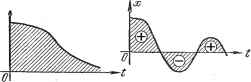

Рис. 8.19.

Z (р) = J ж {t) е-Р* dt.

Отсюда следует, что интеграл (8.53) может быть найден посредством предельного перехода р 0:

оо оо

( X {t) dt = lim ( ж {t) е-Р dt = lim X (p).

(8.54)

Неудобством интегралыюи оценки вида (8.53) является то, что опа годится только для монотонных процессов, когда не меняется знак отклонения ж. Если же имеет место колебательный процесс (рис. 8.19, б), то при вычислении интеграла (8.53) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем регулирования может быть неизвестна, то применять интегральную оценку вида (8.53) оказывается практически нецелесообразным. Поэтому предлагалась другая интегральная оценка:

! = j I ж I ,

(8.55)

т. е. сумма абсолютных величин всех площадей по кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.

Квадратичная интегральная оценка. В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке, называемой иногда квадратичной площадью регулирования:

I=xdt (ж-0 при f- оо), (8.56)

.0 .

которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).

Величина / (8.56) будет тем меньше, чем меньше сумма заштрихованных на рис. 8.20 площадей (взятых для квадратов ординат), т. е. чем лучше

переходный процесс приближается к идеальному скачку регулируемой величины вслед за скачком задающего или возмущающего воздействия. Ниже будет показано, что такая оценка не всегда является лучшей, но пока остановимся на ней.

Заметим, что оценку (8.56) называют также квадратичной динамической ошибкой регулирования. Ее можно записать в безразмерном виде:

(8.57)

где X = X (t) обозначает отклонение регулируемой величины в переходном процессе от еенового установившегося значения: х {t) = у {t) - у (оо);

С - некоторая величина, имеющая размерность регулируемой величины, например статическое отклонение у (оо); Qq - среднегеометрическое значение корня характеристического уравнения (8,26).

Рассмотрим один из возможных способов вычисления квадратичной интегральной оценки (8.56) при скачкообразном внепшем воздействии.

В общем случае дифференциальное уравнение системы автоматического регулирования (в символической оператор-

Рис. 8.20.

ной записи) согласно (5.5) имеет вид

D(p)y(t) = R (р) g (t) - N (р) f (t),

(8.58)

где у (t) ~ регулируемая величина или ее отклонение, g (t) ж f (t) - задающее и возмущающее воздействия.

Степени многочленов R (р) ж N (р) обычно ниже, чем D (р); в некоторых случаях они могут иметь ту же степень, что и полином D (р). Пусть переходный процесс вызывается единичным скачком 1 (t) либо функции / при g == = const, либо функции g при / = const. Положим, например, что рассматриваем скачок задающего воздействия g (t) = 1 (t). Изображение Лапласа

такого скачка будет G (р) = -. Перейдя в формуле (8.58) к изображениям,

получаем

D(p)Y(p)R{p)-L..

(8.59)

Изображение регулируемой величины у (t) представляет собой дробно рациональную функцию:

(8.60)

Отклонение х регулируемой величины от нового установившегося состояния в переходном процессе, входящее в формулу (8.56), будет

{t)=yit)-y(oo) = y(t)-

где у (t) есть решение уравнения (8.59), а также оригинал изображения (8.60).

Для изложенных условий при т <Ц п ниже без вывода приводится формула [121], по которой может быть вычислена квадратичная интегральная

1= Xdt= {Втт + Bm-iAm-1 + ...

О

...+B2A2 + BAi + BoAo)-

(8.61)

где А есть следующий определитель п-го порядка (равный старшему определителю Гурвица, но записанный в несколько иной форме):

(8.62)

На границе устойчивости А = О и / схэ.

Через Ajj (к = т, т - 1, . . ., 2, 1,0) в формуле (8.61) обозначены определители, получающиеся путем замены в определителе (8.62) (т - к + + 1)-го столбца столбцом

71-1

(8.63)

Коэффициенты Б, £ -1, . . . вычисляются по формулам:

Вщ = bmi

Вт-1 - Ьт-1 - 2ibjyibm-2i

Вт-2 = Ь г-2 - 2bm-ibm-3 + 2bmbm-k,

(8.64)

Bu=bl-2bu+ibk-i + 2bft+2fcft-2 + ... -f 2 (-1)bmbh-m.

В определителе (8.62) заменяются нулями все буквы с индексами меньше нуля и больше п, а в формулах (8.64) - с индексами меньше нуля и больше т.

В том случае, когда т = п, формула (8.61) заменяется следующей:

/= J xdt = -{Br.An + B.,An-i+ ... +BlA2 + B[At) - . (8.65)

оцешса: