Существенное значение имеет взаимное расположение вещественного и комплексных корней. Будем различать здесь два случая: / - пара комплексных корней лежит ближе к мнимой оси, чем вещественный, и 77 - вещественный корень лежит ближе к мнимой оси, чем пара комплексных. Границей между этими двумя случаями является расположение всех трех корней на одинаковом расстоянии от мнимой оси. Уравнение этой границы можло найти, положив значения корней =- а и да, з = - ± /р. Тогда

характеристическое уравнение (8.49) будет

+Aq\-\-Bq + 1 =

== (а + а) (9+ а-7Р) (9 + а + /Р) = = g+Зag-Ь(Зa-Ьp)§ +

+ а{а + р2) = 0.

Уравнивание коэффициентов при одинаковых степенях дает Л = 3а, Б = 3a2-f-p 1=а (a-pj,

В результате совместного решения последних трех равенств получаем после исключения аир искомое уравнение, ; соответствующее граничному случаю:

2А - 9Л5 + 27 = О, А< 3.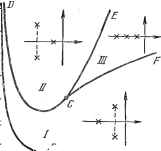

4 6 6

Рис. 8.15.

Написанное равенство дает на плоскости параметров кривую CD. В результате область устойчивости разбивается на три части: 7, 77, 777 (см. рис. 8.15). Этот график называется диаграммой Вышнеградского. Он построен им в 1876 году в работе, которая положила начало развитию теории

Рис. 8.16.

автоматического регулирования. На рисунке показан характер расположения корней внутри каждой из этих частей области устойчивости.

В области 777, где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных на третьем графике рис. 8.16. Область 777 носит название области апериодических процессов.

В областях 7 и 77, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 8.16. В области 7 быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей. Это будет область колебательных процессов. В области 77, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.

Диаграмма Вышнеградского получила дальнейшее развитие. Для более точной оценки характера переходного процесса на ней можно нанести вспомогательные линии, разбивающие области 7, 77 и 777 на еще более мелкие части, что позволяет при известных параметрах Вышнеградского иметь более

полное суждение о быстродействии и запасе устойчивости. Ниже будут рассмотрены наиболее распространенные способы уточнения диаграммы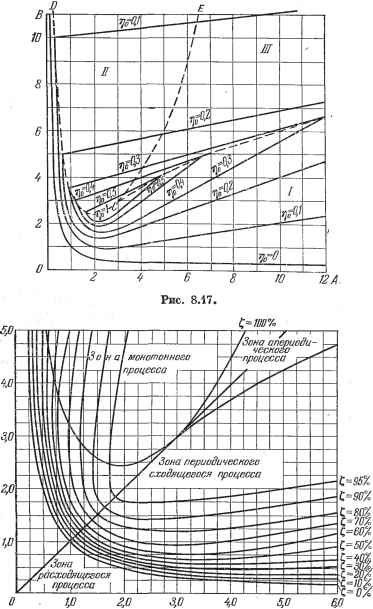

Рис. 8.18.

Вышнеградского посредством нанесения линий равной степени устойчивости (для оценки быстродействия) и линий равного затухания (для оценки запаса устойчивости).

ij Для нанесения линий равной степени устойчивости обратимся к нормированному характеристическому уравнению (8.49). Для получения смещенного уравнения введем новую переменную, определяемую соотношением q = - Цо, где т]о обозначает степень устойчивости для нормированного

Смещенное уравнение имеет вид

<й + Aql + Aq + = 0. (8.50)

Коэффициенты этого уравнения:

1 = -3ilo -VA, А2 = Зц1 - 2Ацо + 5, 3 = -0 -Ml -5 + 1.

Применим к смещенному уравнению условие границы устойчивости. Колебательная граница устойчивости, соответствующая чисто мнимым корням смещенного уравнения (8.50), будет при выполнении условия А-А. ~ ~ Ад. Апериодическая граница устойчивости (нулевой корень) будет при Ад = 0. Первое условие при подстановке значений коэффициентов приводит к уравнению

В--А + По{А-2цо), (8.51)

а второе дает

B = Ario-ii + -. (8.52)

На основании полученных уравнений, задаваясь различными значениями 1]о = const, можно построить на диаграмме Вышнеградского линии одинаковых значений нормированной стенени устойчивости (рис. 8.17). По уравнению (8.51) построены кривые т]о = const в области /, так как там, согласно рис. 8.15, ближайшими к мнимой оси являются комплексные корш!. Кривая 1)о = О совпадает с границей устойчивости. Уравнение (8.52) дает прямые, которые нанесены в областях и /.

Как видно из диаграммы, наибольшая степень устойчивости щ = i имеет место в точке С с координатами А = 3 ж В = 3. Следовательно, эта точка соответствует наилучшим значениям параметров с точки зрения величины степени устойчивости. Однако, как уже отмечалось, степень устойчивости является приближенной оценкой быстроты затухания переходного процесса. Позтому при выборе параметров системы регулирования практически нет смысла попадать именно в эту точку диаграммы. Можно считать, что наилучшей областью параметров системы будет область, прилегающая к точке С, например внутри замкнутой кривой = 0,5.

На рис. 8.18 приведена диаграмма Вышнеградского с нанесенньши линиями равного затухания 1, = const. (Аналитические выкладки не приводятся ввиду громоздкости). Эти же линии являются, по существу, и линиями 1завной колебательности (.i = const, так как колебате-тхьность и затухание связаны между собой формулами (8.41) и (8.42).

§ 8.8. Интегральные оценки

РХнтегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина

Ii=x{t)dt, . (8.53)

уравнения. Для исходного уравнения (8.47) согласно (8.48) степень устойчивости будет