
 |
|
|
Главная -> Логарифмическое определение устойчивости Через один период Т - 2я Затуханием за период называют величину f - л ь- г. - г. (8.40) Эта величина обычно выражается в процентах. Подставляя значение амплитуды Сг, получаем =1-е 1, . (8.41) (8.42) Обычно в системах автоматического регулирования допускается затухание за один период не менее чем 90 ч- 98%. Так, например, если % =98%, то допустимая колебательность при этом , составит In 50 = = 1,57. Соответственно при g = 90% получаем ц 2,72. Задание определенной колебательности заставляет ограничивать область расположения корней двумя лучами (рис. 8.14, а), которые составляют с осью вещественных угол Ф = arctg - = arctg [х. (8.43) - 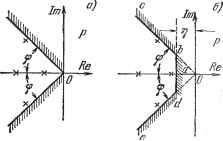 Рис. 8.14. Колебательность системы можно определить без нахождения корней характеристического уравнения подобно тому, как это было сделано вьппе по отношению к степени устойчивости. Идея метода заключается в том, что используется подстановка р = jze~J, которая соответствует повороту коор- динатных осей (рис. 8.14, б) против часовой стрелки на угол ф. При этом по крайней мере один корень попадает на ось мнимых и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения. При задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной прямой, проходящей параллельно оси мнимых на расстоянии т] (рис. 8.14, б). Расположению корней в этой области соответствует выдерживание требуемого запаса устойчивости, определяемого величиной, колебательности ц или затуханием, и требуемой степени устойчивости т], характеризующей быстродействие системы. Для определения параметров системы, при которых обеспечивается нахождение корней характеристического уравнения в заданной области, можно воспользоваться 1)-разбиением. В этом случае в плоскости двух параметров системы может быть построена область, аналогично построению области устойчивости (см. § 6.4). Напомним, что при построении области устойчивости комплексная величина р = /со изменялась от -]сх> до +700, что соответствует движению по мнимой оси снизу вверх. В рассматриваемом случае комплексная величина р должна перемещаться по границе допустимого расположения корней edabc (рис. 8.14, б). В силу симметрии области достаточно рассмотреть участок аЪс. Методика построения допустимой области изменения двух параметров системы А и В, входящих линейно в характеристический полином D (р) = йоР + ад - 4- . . . + п, остается аналогичной, за тем исключением, что для участка аЬ делается подстановка р = -т] + jco, а затем частота изменяется в пределах О <; со <; IT tg ф = mi. Для участка be делается подстановка р = - - + /со и часто- та изменяется в пределах т]р, со < +оо. Использование корней характеристического уравнения для оценки качества регулирования является не совсем полным, так каквид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения. Для того чтобы учесть это обстоятельство, рассмотрим, например, зависимость между регулируемой величиной и управляющим воздействием, записанную посредством передаточной функции замкнутой системы (5.18): Yip) = 0{p)G{p) = j-G{p). Передаточная функция замкнутой системы представляет собой дробно-рациональную функцию Раскладывая числитель и знаменатель (8.44) на множители, получим а iPr-Pi) (Р-Р) (Р-Рп) Корни числителя pj, . . ., рт называются нулями передаточной функции, так как в точке р = pi передаточная функция обращается в нуль. Корни знаменателяр, . . ., рп являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе, т. е. при р = Pi, передаточная функция обращается в бесконечность. Полюсы передаточной функции характеризуют левутю часть дифференциального уравнения, а нули - правую. В частном случае, когда передаточная функция (8.44) не имеет нулей, правая часть дифференциального уравнения имеет вид В {р) у (t) = bmf (t) и формула (8.45) сводится к выраженшо М = ..(Р-й)(Р- р.)...(Р-я..)- , < - В этом случае вид переходного процесса определяется только расположением полюсов. Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. Не останавливаясь на подробном анализе, приведем без доказательства общие рекомендации, которых желательно придерживаться при выборе расположения полюсов и нулей передаточных функций [98]. 1. Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от области полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе. 2. Для уменьшения отклонений в переходном процессе часто бывает выгодно удалять полюсы друг от друга. называются параметрами Вышнеградского. На плоскости параметров А ш В нанесем границу устойчивости. Условия устойчивости системы третьего порядка были впервые сформулированы Вышнеградским еще в 1876 году, до появления в 1895 году критерия Гурвица. Эти условия: .Л > О, 2? > О и АВ > 1. Уравнение границы устойчивости (колебательной): АВ = 1 при Л > О и Б > 0. Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 8.15) Область устойчивости системы, согласно написанным выше условиям, лежит вьпце этой кривой. Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического уравнения. Заметим, что в точке С, где А = 3 м В = д, характеристическое уравнение (8.49) принимает вид (q + 1) = 0. Следовательно, в этой точке все три корня равны: 91 = 92 = 9s = -1- При этом для исходного характеристического 3 /- уравнения согласно (8.48) получаем Pi = Р2 = Ps = - / = -о- В общем случае возможны два варианта: 1) все три корня вещественные; 2) один корень вещественный и два комплексных. Граница между этими двумя случаями определяется равенством нулю дискриминанта уравнения третьей степени (8.49), который может быть получен, например, из формулы Кардана для решения кубического уравнения АВ - 4(А + В + 18АВ - 27 = 0. Это уравнение дает на плоскости параметров А, В две кривые: СЕ и CF (рис. 8.15). Внутри области ECF дискриминант положителен. Следовательно, в этой области имеется три вещественных корня (область /). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары комплексных корней. 3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси. Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованиями обеспечения определенного запаса устойчивости и быстродействия (см. рис. 8.14, б). § 8.7. Диаграмма Вьппнеградского Рассмотрим характеристическое уравнение третьего порядка аоР + (hP -i- агр -Ь Og = 0. (8.47) Приведем его к нормированному виду. Для этого разделим все члены на йд и введем новую переменную = рУ=-Щ (8.48) Здесь использовано понятие среднегеометрического корня (8.26): в результате получим нормированное уравнение + Ад + Bq + i = О, (8.49) где коэффициенты
|