процессов, а накладывая определенные условия на корни характеристического уравнения.

Пусть характеристическое уравнение системы имеет вид

щр + + . . . + йьр - + . . . + + = о, (8.25)

где j5 = с + /со - комплексное число.

Используя понятие среднегеометрического корня

где Pi, -i Рп - корни характеристического уравнения, в формуле (8.25) можно перейти к новой комплексной величине q путем подстановки р = Q(,q- в результате получим уравнение

+ Aq- + . . . + AkP + . . . + A.q + 1=0, (8.27)

в котором безразмерные коэффициенты А-, А . . Ат, . . А-г определяются выражением

(8.28)

= и т. д.

а его корни равны qx--i иа - п

Исходное характеристическое уравнение (8.25) при возвращении к прежней комплексной величине получает вид

р + А,р- + . . . + AQ- р-- + . . . -Ь Q = 0. (8.29) Среднегеометрический корень Qo может служить мерой быстроты протекания переходных процессов. Если в уравнении (8.29) увеличить йд, например, в 10 раз, то на основании теоремы подобия (табл. 7.2) переходный процесс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее.

В связи с этим можно рассматривать (8.27) как некоторое нормированное характеристическое уравнение, которому соответствует переходный процесс, построенный для безразмерного времени Ц = Qj,. Если качество переходного процесса является приемлемым с точки зрения допустимого запаса устойчивости, определяемого, например, перерегулированием (рис. 8.3), то требуемая быстрота протекания переходного процесса может быть обеспечена соответствующим выбором величины Оо-

Для увеличения величины Оо, как следует из (8.26), необходимо увеличивать свободный член характеристического уравнения й . Напомним, что в статических системах й = 1 + if, а в астатических й = К, где К - общий коэффициент усиления по разомкнутой цепи регулирования. Следовательно, повышение быстродействия может осуществляться за счет увеличения общего коэффициента усиления.

Для оценки быстродействия системы может использоваться понятие степени устойчивости ).

Под степенью устойчивости т] понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 8.12). Здесь могут

1) Термин степень устойчивости не является удачным, и его, вообще говоря, следовало заменить термином степень быстродействия . Это объясняется тем, что степень устойчивости никак не связана с удалением системы от границы устойчивости, определяемым по склонности системы к колебаниям. Однако этот термин используется в литературе, и мы будем его придерживаться.

быть два случая: когда ближайший корень является вещественным (рис. 8.12, а) и когда к оси мнимых ближе всего расположена пара комплексных корней (рис. 8.12, б).

Корни характеристического уравнения, расположенные ближе всего к оси мнимых, т. е. имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе (7.3) члены, которые затухают наиболее медленно. В большинстве случаев переходный процесс можно считать закончившимся тогда, когда затухнет член, определяемый ближайшим к мнимой оси корнем. Если ближайшим к мнимой оси является вещественный корень, то составляющая в переходном процессе, определяемая этим корнем, будет иметь вид Жг, (t) = Се .

Положив в конце переходного процесса (tj) = ACj, где Д = 0,01 0,05, можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса:

tUn. (8.30)

Так, например, если принять Д = 0,05, то время переходного процесса составит

. 1 , 1 3

Если ближайшей к оси мнимых является пара комплексных корней -11 ± /р, то составляющая в переходном процессе, определяемая этими корнями, будет (t) = С,]е п* sin ф1 + я])).

Положив в этом случае х (t) = ДСг нельзя в общем виде определить время переходного процесса, так как для этой цели потребовалось бы решить трансцендентное уравнение. Однако можем найти верхнюю границу переходного процесса, положив в этом уравнении sin (P;f я])) = 1. Тогда получим выражение

*п<1п4:- {8-31)

Таким образом, и в этом случае величина степени устойчивости будет в какой-то мере определять быстроту затухания переходного процесса.

Более строго связь между видом переходного процесса и величиной степени устойчивости может быть определена для случая, когда исходное дифференциальное уравнение системы имеет вид

(йоР + ад - + ... + an)xit)=f{t). (8.32)

Тогда можно показать [61], что при всех вещественных корнях или одной паре комплексных корней для переходной функции справедливо неравенство

i + v{t], f)>h{t)>i-v (т], t), (8.33)

где 1 -Ь у (т], t) - функция, ограничивающая h {t) сверху (мажоранта); 1 - у (f], t) - функция, ограничивающая h {t) снизу (миноранта). Вспомогательная функция v {\[, f) определяется из выражения

.(г 0 = - + . - . (8.34)

Миноранта совпадает с переходной функцией, если характеристическое уравнение имеет корень = -т] кратности п, т. е. выглядит следующим образом:

йоР + ад - + . . . -Ь й = й (Р + 1]) = 0. (8.35)

Очевидно, что в этом случае п-кратный корень совпадает со среднегеометрическим корнем

= о=К- (8-36)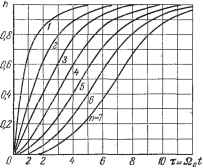

Рис. 8.13.

Из неравенства (8.33) вытекает, что при заданном значении среднегеометрического корня Qo = const и всех вещественных корнях наименьшее время переходного процесса будет при всех кратных корнях, т. е. в случае (8.35).

На рис. 8.13 приведены миноранты, совпадающие с переходными характеристиками для случая п-кратного корня, построенные в функции относительного времени т = Qot для различных значений порядка дифференциального уравнения п.

Важным обстоятельством является то, что степень устойчивости можно найти без вьгаисления значений корней характеристического уравнения. Для этой цели в характеристическом уравнении (8.25) переходят к новой переменной z = р +7]. Подставляя в него р = z - т], получаем так называемое смещенное уравнение

ао (Z - -пГ + 1 (Z - -0) - + . - . +

-Ьй 1 (z - т)) -Ь й = 0.

Раскрывая скобки и группируя подобные члены, получаем

az+AiZ-+... + An-iz+ An= 0. (8.37)

Это уравнение соответствует смещению осей на плоскости корней (рис. 8.12) влево на величину т]. В результате один (рис. 8.12, а) или два (рис. 8.12, б) корня попадают на ось мнимых, что соответствует границе устойчивости.

Для вычисления степени устойчивости необходимо применить к смещенному характеристическому уравнению (8.37) любой критерий устойчивости и определить, при каком значении т] получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство нулю свободного члена характеристического уравнения:

тг = й - + Й 2Т]2 - йп-з-П +...== О, (8.38)

а колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица, прохождение кривой Михайлова через начало координат и прохождение амплитудно-фазовой характеристики разомкнутой системы через точку (-1, /0).

Обратимся теперь к оценке запаса устойчивости системы автоматического регулирования. Склонность системы к колебаниям будет наблюдаться, если в решении характеристического уравнения будут присутствовать комплексные корни вида -а ± /Р- Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью:

а

(8.39)

Колебательность связана с другим корневым показателем запаса устойчивости - с так называемым затуханием. Комплексные сопряженные корни дают в выражении для переходного процесса член вида

X (t) = Се- * sin it -Ь If).

Найдем затухание амплитуды синусоидального колебания за один период. При некотором времени 1 = 1 эта амплитуда равна

Ci = Ce- * .