Передаточная функция по ошибке

ф -.- T,T2P+(Ti + T2)T + P

Деля числитель па знаменатель, получаем ряд Сравнение этого ряда с (8.19) дает

Так, например, если задающее воздействие в этой системе меняется по закону

git)go + Vot + , то установившаяся ошибка будет

%от = +[ (Г.-Ь Г) - 11.

получить делением числителя на знаменатель и сравнением получающегося ряда с выражением (8.19).

Коэффициент Со может быть отличным от пуля только в статических системах и то только в тех случаях, когда не принимаются меры по устранению первой составляющей статической ошибки посредством масштабирования или использования неединичных обратных связей (см. § 9.3).

В системах с астатизмом первого порядка Со = О, а коэффициент q связан с добротностью по скорости соотношением

ci-. (8.21)

В системах с астатизмом второго порядка

Со = О и = О, а коэффициент Cj связан с добротностью по ускорению соотношением

1 = -- (8-22)

При исследовании ошибки от возмущающего воздействия можно получить все коэффициенты не равными нулю при астатизме любого порядка, так как астатизму по задающему воздействию может соответствовать наличие статической ошибки по возмущению.

Если задающее воздействие g (t) имеет ограниченное число производных, то ряд (8.20) будет иметь ограниченное число членов. Предположение, что коэффициенты ошибок представляют собой постоянные числа, обусловливает применение этого метода для сравнительно медленно меняющихся входных воздействий g (t) или / (t), когда можно пренебречь влиянием переходной составляющей процесса и рассматривать только вынужденное движение системы.

Пример. Определим первые три коэффициента ошибки по задающему воздействию, если передаточная функция разомкнутой системы имеет вид

§ 8.4. Определение запаса устойчивости и быстродействия по переходной характеристике

Оценку запаса устойчивости и быстродействия можно произвести по виду кривой переходного процесса в системе автоматического регулирования при некотором типовом входном воздействии, которым может быть как задающее, так и возмущающее воздействие. В качестве типового входного воздействия рассматривается обычно единичный скачок. В этом случае кривая переходного процесса для регули-

руемой величины будет представлять собой переходную характеристику системы (рис. 8.3). Она может строиться для регулируемой величины у {{) или для ошибки X {t).

Склонность системы к колебаниям, а следовательно, и запас устойчивости могут быть охарактеризованы максимальным значением регулируемой величины Утаи. или так называемым перерегулированием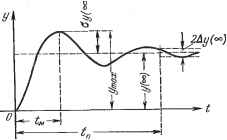

J/ (оо)

Рис. 8.3.

(8.23)

где у (оо) Ф О представляет собой установившееся значение регулируемой величины после завершения переходного процесса. 0=

Допустимое значение перерегулирования для тойили иной системы автоматического регулирования может быть установлено на основании опыта эксплуатации подобных систем. В большинстве случаев считается, что запас устойчивости является достаточным, если величина перерегулирования не превышает 10 30%. Однако в некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, т. е. был монотонным; в ряде других случаев может допускаться перерегулирование 50 4-70%.

Быстродействие системы может определяться по длительности переходного процесса ц. Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство

у(0-у (оо) К Ду(сю) = Д1, . (8.24)

где Ai - заданная малая постоянная величина, представляющая собой обычно допустимую ошибку. Величина у (оо) в частном случае может равняться нулю.

Допустимое значение времени переходного процесса определяется на основании охЕыта зксплуатации систем регулирования. В следящих системах в качестве единичного скачка принимается мгновенное изменение управляющего воздействия g (if) = 1 {t). В этом случае под величиной Д обычно понимают некоторую долю входного воздействия, составляющую, как правило, от 1 до 5% величины скачка на входе.

Иногда дополнительно к величине перерегулирования а% (или к вели- пане Ушах) задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Это число составляет обычно 1 -т- 2. В некоторых системах колебания могут вообще не допускаться, а иногда может допускаться до 3 4 колебаний.

Графически требования к запасу устойчивости и быстродействию сводятся к тому, чтобы отклонение регулируемой величины не выходило при единичном входном воздействии из некоторой области, изображенной

на рис. 8.4. Эта область называется областью допустимых отклонений регулируемой величины в переходном процессе.

В следящих системах удобно применять сформулированные требования качества к ошибке системы х (t) = g (t) - у (t). В этом случае можно рассматривать область допустимых значений ошибки и при более сложных входных воздействиях, например при мгновенном приложении па входе постоянной скорости.

Дальнейшее развитие критериев качества, использующих переходную характеристику, приводит к введению дополнительных оценок качества (кроме введенных выше tj Утах и о%). К ним относятся следующие оценки.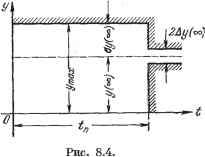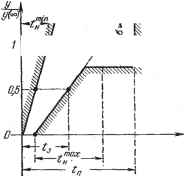

Рис. 8.5.

1. Время запаздывания its, равное отрезку времени, заключенному между моментом приложения входного скачкообразного сигнала и моментом времени, при котором осредненная выходная величина становится равной половине ее установившегося значения. Примененный здесь термин осредненная означает, чТо в случаях, когда па передний фронт выходного сигнала накладываются высокочастотные колебания (это может иметь место в системах высокого порядка), величина 4-определяется по сглаженной кривой, аппроксимирующей реальную переходную характеристику системы.

2. Время нарастания <н равное отрезку времени, заключенному между точкой пересечения оси времени с касательной, проведенной к осредненной кривой переходной характеристики в точке i = 4, и координатой t точки пересечения указанной касательцой с горизонтальной прямой, соответствующей установившемуся значению регулируемой велич1шы. Максимальное время нарастания ограничивается требуемым быстродействием. Минимальное время нарастания н ограничивается допустимыми в системе ускорения и колебательными режимами.

Уточненная диаграмма качества переходного процесса изображена на рис. 8.5.

§ 8.5. Приближенная оценка вида переходного процесса по вещественной частотной характеристике

Построение кривой переходного процесса является в большинстве случаев весьма трудоемкой операцией. Позтому целесообразно использовать методы, позволяющие определить вид переходной характеристики без построения всей кривой процесса. Это можно сделать по вещественной частотной характеристике Р (со) замкнутой системы, которая используется для построения переходной функции (см. § 7.5). При этом предполагается, что